Advanced fault-tolerant visual multi-secret sharing scheme
Abstract
Aim: In visual cryptography, a secret image is encrypted into two meaningless random images called shares. These two shares can be stacked to recover the secret image without any calculations. However, because of the alignment problem in the decryption phase, risk of poor quality of the restored image exists. Encrypting multiple secrets on two images simultaneously can improve execution efficiency.
Methods: Let 7 × 7 pixels be a unit; this paper designs a codebook for any unit in the secret images by using a random grid. Besides, this paper shows a general shifting approach that can embed N (≥ 2) secret images simultaneously with adjustable distortion.
Results: This paper provides a visual multi-secret sharing scheme without pixel expansion; the proposed scheme can encrypt more than two secret images into two shares simultaneously. During decoding, aligning the shares precisely is not necessary.
Conclusion: Theoretical analysis and simulation results indicate the effectiveness and practicality of the proposed scheme.
Keywords
INTRODUCTION
A secret-sharing scheme (SSS) is ideal for storing information and is highly essential for ensuring information security. The primary idea behind an SSS is that a secret is distributed among a group of participants, among whom only qualified participants can reconstruct the secret. A visual SSS (VSSS) is also crucial for information security, and its most attractive feature is that the confidential content in a secret image can be deciphered by the human visual system. Compared with an SSS, a VSSS requires no computation in the decoding phase; therefore, a VSSS is widely applicable in many fields. In 1994, Noar and Shamir [1] first developed the concept of visual cryptography (VC), and they demonstrated a
The performance of the
Encoding more than one image simultaneously is efficient with respect to time and space costs. Several studies have proposed and discussed schemes for encoding multiple images simultaneously[10-27]. The scheme proposed by Shyu[10] in 2009 is an extension of that proposed by Shyu[3] in 2007, which can encode two images simultaneously. In 2008, Chen et al.[11] proposed an RG-based visual multi-SSS (VMSSS) that entails using a rotating RG to encode two images into two shares. Furthermore, Chen et al.[12] presented another VMSSS that can embed four secret images into two shares by using four specific angles, namely
In VC, each share can be printed on a separate transparent sheet, and each input image can be decrypted by overlapping these shares. However, if the scheme lacks fault tolerance, then the reconstructed image may have severely poor visual quality in the event of misalignment. In 2002, Nakajima and Yamaguchi[21] proposed an enhanced VSS scheme that allows slight misalignment by reserving some space for fault tolerance. On the basis of the idea presented by Nakajima and Yamaguchi[21], Juan et al. proposed two schemes with no pixel expansion in 2016[22] and 2018[23], respectively. Al-Tamimi and Gaafar[24] designed a scheme that entails using four-pixel blocks to encrypt a secret. Although no pixel expansion occurred, they did not discuss a security analysis of their scheme. In 2016, Lin and Juan used the ideas described by Chang and Juan[14] in 2012, and Juan et al.[22] in 2016 to propose an advanced scheme[25] that can encode two images into two shares, and the images can be reconstructed by stacking two imperfectly aligned shares. In the present paper, we combine the ideas presented by Chang et al.[15] in 2018, and Juan and Chen[23] in 2018 and propose a fault-tolerant multi-SSS that encodes more than two secret images into two shares simultaneously without pixel expansion.
The rest of this paper is organized as follows. Related work and the proposed scheme are presented in Sections 2 and 3, respectively. The experimental results are presented in Section 4. Analysis and comparisons are presented in Section 5.
RELATED WORK
In 1987, Kafri and Keren[2] first introduced the idea of RG that can be used to classify any pixel in an image as black (opaque) or white (transparent). An imager pixel
The transmittance of an image
Stacking results of two pixels
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Transmittance in KK1
| Probability | |||||
| 1/2 | 1/2 | ||||
| 1/2 | |||||
| 1/2 | 0 | ||||
| 1/2 |
KK1 algorithm (proposed in [2])
Input: secret image with size
Output: two cipher-shares
Generate an
Return
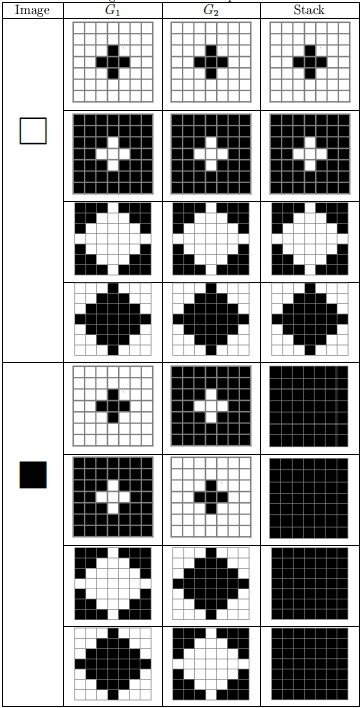
Using the basic model of VC first introduced by Noar and Shamir[1], Nakajima and Yamaguchi[21] proposed a fault-tolerant scheme with pixel expansion in which diamond patterns are designed for encoding; this allows slight deviations during stacking while enabling the classification of the original color of the secret image. In 2016, Juan et al.[22] proposed a fault-tolerant scheme without pixel expansion. This scheme considers
Figure 1. Designed patterns for
Transmittance for
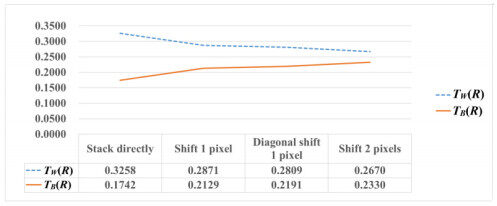
| Stack | Shift 1 pixel | Shift 2 pixels | Diagonal shift 1 pixel | |
| 1/2 | 73/196 | 60/196 | 69/196 | |
| 0 | 25/196 | 38/196 | 29/196 |
With respect to RG, Lin and Juan[25] proposed a visual two-secret sharing scheme with no pixel expansion; the scheme has fault-tolerant mechanisms and combines the advantages of Juan et al.'s scheme[22] and Chang and Juan's scheme[14]. The encryption phase is divided into three parts, namely scale down, encryption, and tolerance. In the scale down part, an input image of size
For multiple-image encryption, Chen et al.[12] proposed a scheme that encodes four secret images into two square shares. Through a rotating mechanism, the four confidential secret images can be restored by stacking one share on the other share after rotating by
We briefly introduce Chang and Juan's scheme[14] that encodes two images into two shares. The main idea of the algorithm[14] is as follows. Two images are divided into
In the
Figure 2. The diagram of the processes in the encryption phase of the VMSSS[15] for
The study by Chang et al.[15] is an extension of Chang and Juan's scheme[14]; the schemes proposed by both studies involve the same recovery operation. During the restoration of secret images
On the basis of the ideas presented in Chang et al.'s scheme[15], and Juan and Chen's scheme[23], we propose a more advanced scheme than Lin and Juan's scheme[25]. Specifically, our proposed scheme uses design patterns[23] to ensure fault tolerance and encrypts multiple secret images by shifting the RG. The scheme is introduced in detail in the next section. To make the relationship between the above schemes clearer, we list them in Table 4.
The relationship between the proposed scheme and some related schemes
| Has | Has lower fault-tolerantmechanisms | Has higher fault-tolerantmechanisms | |
| Kafri and Keren[2] | Juan et al.[22] | Juan and Chen[23] | |
| Noar and Shamir[1] | |||
| Chang and Juan[14] | Lin and Juan[25] | ||
| Chang et al.[15] |
OUR SCHEME
In this section, we describe the proposed scheme for encrypting multi-secret images by shifting RGs through a fault-tolerant mechanism. Therefore, the proposed scheme can be denoted as fault-tolerant RG-based VMSSS (FT-VMSSS).
In our scheme, there are four functions and one procedure that help us build the main algorithm. The first three functions are defined as follows. They are used below in the procedure and main algorithm.
Definition 1.
Definition 2.
Definition 3.
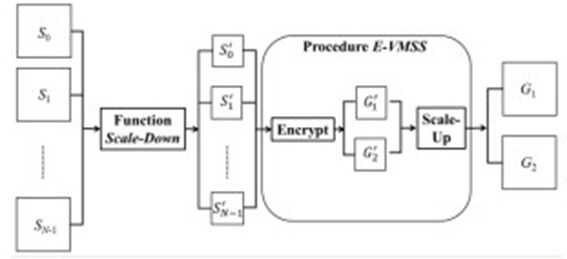
Figure 3 shows the model of the proposed encrypt method. The main concept of our approach is as follows: first, we divide each secret image into several blocks with pixels of size
Therefore, using the Scale-Down function, we obtain
Notations used in the algorithm FT-VMSS and procedure E-VMSS
| : Number of secret images. | |
| : Secret image | |
| : A positive integer that must be a positive factor of | |
| : Scaled-down image | |
| : A random number among | |
| ( | : A random position determined by |
| : Pixel value of image | |
| % | : Modulus operation. |
| : Reduced share | |
| X | : A random pattern |
| : Share |
Encryption phase
Function 1. (
Input: a secret image
Output: one pixel of the input secret image
Function 2. (
Input: a pixel of secret image
Output: a pixel of shares
Function 3. (
Input: a pixel of secret image
Output: a pixel of the other share
Function 4. (Scale-Down)
Input: the original secret image
Output: the scaled down image
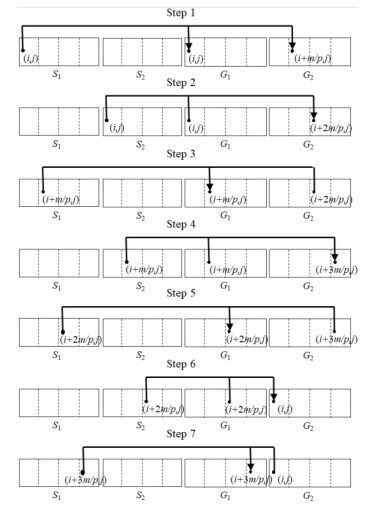
Procedure E-VMSS (
One pattern
for (int
for (int
Algorithm FT-VMSS
Input: Secret images
Output: Shares
for(
Repeat
Until all the pixels of
Decryption phase
After collecting the two cipher-grids
EXPERIMENTAL RESULTS
This section describes three experiments performed in this study. In the first experiment, we encoded three images into two shares, where the size of the input images was
Figure 4. Results of Experiment 1: (A-C) secret images; (D) share
In the second experiment, four images with pixels of size
Figure 5. Results of Experiment 2: (A) secret image; (B) share
In the third experiment, images with pixels of size
ANALYSIS AND CONCLUSIONS
In this paper, we present the design of an FT-VMSSS for sharing multiple secret images simultaneously, as described in Section 3. In the proposed scheme, multiple secrets can be embedded into two cipher shares, and the distortion is evenly distributed across the two shares.
Let
Therefore, when
Through the encryption process described in Section 3 and Chang et al.'s scheme[15], we can calculate the distortion of the restored images
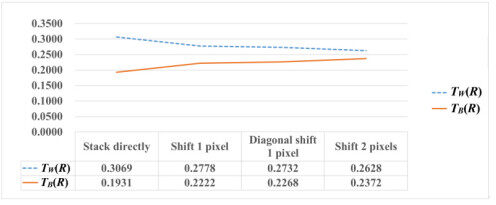
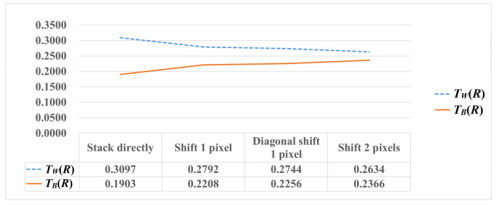
According to our experimental results, fault-tolerant performance can permit a shift of only one pixel. Figures 7-9 indicate that, for the transmittance analysis for sharing three or four secret images, p = 7 or 20, the difference between white and black transmittance decreased gradually from the case of perfect stacking to that of imperfect stacking (but
Table 6 presents a comparison of the performance of our scheme and those of schemes proposed in related studies. Among the schemes proposed in related studies, those with a fault-tolerant mechanism can encrypt at most two secret images at a time, and those that can encrypt any multiple secret images lack the mechanism of fault tolerance. Our scheme is the first MVSSS to be fault-tolerant and can really encrypt any number of secret images. Therefore, compared with these schemes, our scheme is more practical.
Comparison of related schemes to the proposed scheme
DECLARATIONS
Authors' contributions
Conceived the proposed idea, provided the main plan and supervised the entire project: Juan JS-T
Contributed in performing the experiments and analyzed the results: Lin JY
Participated in the experiment and drafting the manuscript: Huang BY
Corrected some deficiencies in the main scheme and assisted in revising the article: Chung YC
All authors discussed the main idea and scientific contribution.
Availability of data and materials
Not applicable.
Financial support and sponsorship
This work was supported by the Ministry of Science and Technology of the Republic of China under Contract (MOST 108-2221-E-260-008- and MOST 110-2221-E-260-003).
Conflicts of interest
All authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2022.
REFERENCES
1. Naor M, Shamir A. Visual cryptography. In: De Santis A, editor. Advances in cryptology-EUROCRYPT'94. Berlin: Springer Berlin Heidelberg; 1995. p. 1-12.
4. Lin SJ, Lin JC, Fang WP. Visual cryptography (VC) with non-expanded shadow images: hilbert-curve approach. In Proceedings of the IEEE International Conference on Intelligence and Security Informatics, 2008. p. 271-2.
5. Yang CN. New visual secret sharing schemes using probabilistic method. Pattern Recognition Letters 2004;25:481-94.
6. Cimato S, De Prisco R, De Santis A. Probabilistic visual cryptography schemes. The Computer Journal 2006;49:97-107.
7. Lin SJ, Chung WH. A probabilistic model of (t, n) visual cryptography scheme with dynamic group. IEEE Trans Inform Forensic Secur 2012;7:197-207.
8. Wu X, Yang CN. Probabilistic color visual cryptography schemes for black and white secret images. Journal of Visual Communication and Image Representation 2020;70:102793.
9. Yang CN, Wu CC, Wang DS. A discussion on the relationship between probabilistic visual cryptography and random grid. Information Sciences 2014;278:141-73.
11. Chen TH, Tsao KH, Wei KC. Multiple-image encryption by rotating random grids. In Proceedings of Eighth International Conference on Intelligent Systems Design and Applications, 2008. p. 252-6.
12. Chen TH, Tsao KH, Lee YS. Yet another multiple-image encryption by rotating random grids. Signal Processing 2012;92:2229-37.
13. Liu CL, Tsai WJ, Chang TY, Peng CC, Wong PS. Meaningful share generation for (2, 2)-multiple visual secret sharing scheme without pixel expansion. The Computer Journal 2015;58:1598-606.
14. Chang JJY, Juan JST. Multi-VSS scheme by shifting random grids. In Proceedings of World Academy of Science, Engineering and Technology. International Journal of Computer and Information Engineering 2012;6: 1-7.
15. Chang JJY, Huang BY, Juan JST. A new visual multi-secrets sharing scheme by random grids. Cryptography 2018;2:24.
16. Salehi S, Balafar MA. Visual multi secret sharing by cylindrical random grid. Journal of Information Security and Applications 2014;19:245-55.
17. Tsao KH, Shyu SJ, Lin CH, Lee YS, Chen TH. Visual multiple-secret sharing for flexible general access structure by random grids. Displays 2015;39:80-92.
18. Siva Reddy L, Prasad MVNK. Extended visual cryptography scheme for multi-secret sharing. In: Nagar A, Mohapatra D, Chaki N, editors. Proceedings of 3rd international conference on advanced computing, networking and informatics. New Delhi: Springer; 2016. p. 249-57.
19. Wu X, Sun W. Random grid-based visual secret sharing with abilities of OR and XOR decryptions. Journal of Visual Communication and Image Representation 2013;24:48-62.
20. Nag A, Biswas S, Sarkar D, Sarka PP. Secret image sharing scheme based on a boolean operation. Cybernetics and Information Technologies 2014;14:98-113.
21. Journal of WSCG 2002;10:303-10. Available from: https://www.researchgate.net/publication/221546377_Extended_Visual_Cryptography_for_Natural_Images [Last accessed on 27 Apr 2022] ]]>.
22. Juan JST, Chen YC, Guo S. Fault-tolerant visual secret sharing schemes without pixel expansion. Appl Sci 2016;6:18.
23. Juan JST, Chen YC. Extended fault-tolerant visual secret sharing scheme without pixel expansion. In Proceedings of International Conference on Security and Management (SAM), 2018.
24. Al-Tamimi AGT, Gaafar A. A new simple non-expansion algorithm for (2, 2)-visual secret sharing scheme. International Journal of Computer Applications 2015;113:1-5.
25. Lin JY, Juan JST. Fault-tolerant visual 2-secret sharing scheme. In Proceedings of 2017 the 7th International Workshop on Computer Science and Engineering, 2017. p. 517-25.
26. Nakajima M, Yamaguchi Y. Enhancing registration tolerance of extended visual cryptography for natural images. J Electron Imag 2004;13:654.
27. Wang D, Dong L, Li X. Towards shift tolerant visual secret sharing schemes. IEEE Trans Inform Forensic Secur 2011;6:323-37.
28. Yang CN, Peng AG, Chen TS. MTVSS: (M)isalignment (T)olerant (V)isual (S)ecret (S)haring on resolving alignment difficulty. Signal Processing 2009;89:1602-24.
29. Chen SK, Lin JC. Fault-tolerant and progressive transmission of images. Pattern Recognition 2005;38:2466-71.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Juan JT, Lin JY, Huang BY, Chung YC. Advanced fault-tolerant visual multi-secret sharing scheme. J Surveill Secur Saf 2022;3:41-54. http://dx.doi.org/10.20517/jsss.2021.29
AMA Style
Juan JT, Lin JY, Huang BY, Chung YC. Advanced fault-tolerant visual multi-secret sharing scheme. Journal of Surveillance, Security and Safety. 2022; 3(2): 41-54. http://dx.doi.org/10.20517/jsss.2021.29
Chicago/Turabian Style
Juan, Justie Su-Tzu, Jen-Yu Lin, Bo-Yuan Huang, Yu-Chun Chung. 2022. "Advanced fault-tolerant visual multi-secret sharing scheme" Journal of Surveillance, Security and Safety. 3, no.2: 41-54. http://dx.doi.org/10.20517/jsss.2021.29
ACS Style
Juan, J.T.; Lin J.Y.; Huang B.Y.; Chung Y.C. Advanced fault-tolerant visual multi-secret sharing scheme. J. Surveill. Secur. Saf. 2022, 3, 41-54. http://dx.doi.org/10.20517/jsss.2021.29
About This Article
Copyright
Data & Comments
Data
 Cite This Article 10 clicks
Cite This Article 10 clicks















Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.