Adaptive mining difficulty for blockchain to resist selfish mining attack
Abstract
Aim: A blockchain provides data consistency and builds a fair mining environment for a network by using a consensus mechanism such as proof of work (PoW) and proof of stake. However, selfish mining is a well-known mining attack. It can reduce the fairness and destabilize the network, especially for a PoW-based blockchain. Therefore, in this paper, we propose a new approach, named the adaptive mining difficulty adjustment protocol, which can deter a selfish attack.
Methods: We propose using the unit profit as an improved version of the relative revenue, because it is more flexible for calculating the miners’ profits in different periods and can be used to analyze repeated mining games. Based on the unit profit, we propose using the adaptive mining-difficulty adjustment protocol to reduce an attacker’s profit. Our protocol evaluates the effective hash power in a network more accurately and corrects the mining difficulty. Moreover, we introduce the discount factor and model the long-term profit to analyze the impact of a miner’s patience on its future profit.
Results: We used an open-source simulator to simulate the competition between a selfish miner and an honest miner and determined their profits under different protocols. Our experimental results show that our protocol can effectively raise the attack threshold, but it reduces the total network profit if the attacker still attacks. However, the long-term profit model shows that a more patient attacker needs to invest more hash power and pay increased mining costs to maintain its attack.
Conclusion: We conclude that, under our protocol, selfish attackers will tend to become honest miners if their hash power does not exceed the threshold, which means that our protocol can effectively deter selfish attacks and some variants of selfish attacks. Briefly, our protocol can correct the mining difficulty and leads to a more stable and fairer mining environment for a PoW-based blockchain.
Keywords
INTRODUCTION
As one of the most famous distributed systems, blockchain technology has been widely applied in various scenarios due to its security, decentralization, and strong privacy. The first blockchain system, called Bitcoin, was created by Nakamoto[1], who implemented a peer-to-peer electronic payment system based on a cryptographic puzzle without any trusted third party. Any distributed system needs to build a consensus on the network status among nodes to maintain the stability of the system. Bitcoin uses the proof of work (PoW) to guarantee data consistency and maintain the fairness of the network. As a famous consensus mechanism, PoW is simple to implement and has high fault tolerance but consumes a significant amount of computing resources. In recent years, many consensus mechanisms have been proposed to replace PoW in a blockchain (such as proof of stake[2] and distributed proof of stake[3]), but PoW is still widely used due to its strong security. Thus, attacks targeting PoW, such as 51% attacks and selfish attacks, have attracted much attention from researchers.
Compared to a 51% attack, the selfish strategy focuses on breaking the stability and fairness of a blockchain instead of attacking its data consistency. Eyal and Sirer[4] demonstrated that an attacker can obtain extra revenue by applying the selfish strategy in a mining game, if it has more than one-third of the hash power of the network. As a result, a selfish attacker can threaten the revenue of other miners and reduce the fairness of the mining environment[5]. Furthermore, such an attack can have an adverse effect on the blockchain, as honest miners may prefer to exit the network or join the attacker’s pool. The result is that a selfish group may become a majority in the network. If there are fewer honest miners, there may be more malicious attacks against the network, which would incur a huge risk to the stability and decentralization of the blockchain. Therefore, a method of deterring selfish attacks is important for protecting the stability and decentralization of a blockchain.
Bitcoin ensures that the growth of the main chain is stable by adjusting the mining difficulty, but the current protocol for doing this has a major weakness: if any miner executes a selfish attack, the network incorrectly calculates the mining difficulty due to an erroneous evaluation of the network hash power. This occurs because the mining difficulty is adjusted based only on the growth of the main chain and not the number of blocks generated in each period, which can be exploited by a selfish attacker. Therefore, our aim in this study is to improve the current protocol for adjusting the difficulty to protect the interests of honest miners. When using a blockchain, in each mining period, each miner needs to repeatedly consume hash power to gain the right to add a block into the main chain. Thus, it is reasonable to model mining as a repeated game. In previous works, mining has always been represented as a single game, and relative revenue is used to assess the block rewards of miners. However, relative revenue cannot be used in a repeated mining game to dynamically assess a miner’s strategy and the distribution of block rewards. Therefore, we need to design a more accurate and flexible profit function to model a repeated mining game.
In this paper, we propose an improved PoW mechanism that can deter a selfish attack. First, we define the unit profit to improve the relative revenue model. The unit profit is a measure of a miner’s profit in each period when the mining difficulty is adjusted. It incorporates the mining cost and can be used to assess dynamically a miner’s strategy and its profit in a repeated mining game. Based on the unit profit, we analyze the weakness of a selfish attack and propose an adaptive protocol for adjusting the mining difficulty according to this weakness. This approach can provide a more accurate evaluation of the effective hash power in a network, and it calculates the mining difficulty more accurately. Then, we model repeated mining games between an attacker and an honest miner. We assess the security and feasibility of our protocol by analyzing whether the mining game is in a Nash equilibrium. Finally, we use an open-source simulator to model our protocol. Our experimental results verified our theoretical conclusion. In brief, the main contributions of our work are as follows:
●→We define the unit profit to overcome the weakness of using the relative revenue, which cannot dynamically assess a mining game. Additionally, we introduce the discount factor to model a miner’s long-term profit when analyzing the impact of its patience on its future profits.
●→We propose the adaptive mining-difficulty adjustment protocol to protect the stability of a blockchain and deter a selfish attack. This protocol can effectively raise the attack threshold and reduce the attacker’s extra profit, thus establishing a fairer mining environment. Furthermore, our protocol has less impact on network performance and is well compatible with the current protocols.
●→We model a repeated mining game between an attacker and an honest miner using the unit profit. With our protocol, the game reaches a Nash equilibrium such that the attacker gives up the selfish attack strategy, which proves that our protocol is effective and secure.
This paper is organized as follows. In this section, we briefly describe the background, motivation, challenges, and contribution of our research, emphasizing the dangers of a selfish attack to a network and the significance of deterring such an attack. We discuss works related to our research in the second section, including blockchains, selfish mining, and some variants of selfish mining. We present our approach for deterring such attacks in the third section, namely the adaptive mining-difficulty adjustment protocol. In that section, we identify the weakness of a selfish attack. Then, we propose the unit profit and describe our protocol based on the unit profit. We analyze the security of our protocol by modeling a repeated mining game between an attacker and another miner. Additionally, we introduce the discount factor to model the miner’s long-term profit and the impact of its patience on its future profits. In the fourth section, we use an open-source simulator to verify the feasibility of our protocol, and we summarize our results. Finally, we review our work and give our conclusions in last section.
RELATED WORK
Blockchains
As one of the most famous distributed systems, blockchains have received increasing attention and have been widely applied in various fields due to their decentralization, security, and anonymity. Thus, blockchains are frequently used for the IoT[6], electronic voting systems[7], privacy-preserving systems[8], and especially cryptocurrencies. A cryptocurrency uses a blockchain as a decentralized distributed ledger with a cryptographic proof instead of a trusted third party. The core of a decentralized blockchain is a consensus mechanism, which is a fault-tolerant process for determining the validity of transactions and controlling the blockchain. For example, Bitcoin uses PoW to build a consensus among nodes. Nodes must invest their own computing resources to solve a cryptographic puzzle before they are allowed to add a block to the main chain. This mechanism has high fault tolerance and security, but the convergence speed is slow, and it consumes a lot of resources. Therefore, researchers have proposed various consensus mechanisms to replace PoW, such as delegated Byzantine fault tolerance[9], proof of activity[10], and others[11,12]. Pass and Shi[13] proposed the concept of fruit and created a blockchain named FruitChains. Different from Bitcoin, the fruit is used to record transactions, which hang from a block. This system does not require a massive amount of hash power. Note that blocks accept fresh fruits only, which means that a fruit cannot have been mined too long ago and was withheld. Pass and Shi demonstrated that a selfish attack cannot work in FruitChains, but they needed to change the data structure of each block for this scheme, which means that the compatibility of the approach is weak.
Selfish mining
In 2014, Eyal and Sirer proposed a deviant mining strategy that enables miners to destabilize Bitcoin with less hash power than a 51% attack, which they called a selfish attack[4]. They demonstrated that a malicious miner could gain more revenue by secretly maintaining a private chain and wasting the hash power of other miners. Furthermore, the selfish strategy can threaten other blockchain systems that rely on PoW[14-16]. Significantly, following previous work, Sapirshtein et al.[17] optimized the attack so that it further threatened the stability of a blockchain. They used Markov decision processes to analyze selfish mining in detail. This approach is a good fit for modeling Bitcoin mining. In a Markov decision process, the player moves through a discrete state space and focuses on maximizing their reward. Therefore, in this paper, we adopt this model to analyze how blocks are generated.
Several researchers have developed blockchain simulators to simulate a selfish attack, because there are no public datasets on selfish attacks. For example, some studies[18,19] used a Monte Carlo simulator to generate selfish-attack data. Such simulators do not need to compute the cryptographic puzzles. Rather, they construct random numbers that satisfy the probability distribution of the strategy. Unfortunately, most of these simulators are not open source, so we could not adapt them to meet our requirements. To ensure the credibility of our experimental data, we used the simulator developed by Carlsten et al.[20]. This simulator is open source and available from GitHub, and we adapted it to provide more data. It can clearly visualize the execution of various mining strategies, including selfish attacks.
Variants of selfish-mining attacks
Some researchers have completed a deeper analysis of selfish attacks. For example, Nayak et al.[21] introduced a new mining strategy named stubborn mining. In both types of attack, the attacker eventually gives up its private chain if its branch is shorter than the main branch. The difference is that this is done later in stubborn mining compared to selfish mining. Furthermore, an attacker can gain more by combining a stubborn attack with an eclipse attack[22,23]. Carlsten et al.[20] conjectured that the selfish strategy is always profitable against Bitcoin when there is no block reward. Moreover, a blockchain can become more unstable when there are multiple attackers because the competition between attackers further wastes the hash power of the whole network[24-26]. Additionally, a selfish attack combined with other attacks can achieve unexpected results. A fork after withholding (FAW) attack[19] and a self-holding attack[27] are both a combination of a selfish attack and a block-withholding (BWH) attack[28]. These attacks perform better than a selfish attack and have a lower attack threshold, which further threatens the stability of the blockchain. However, a distinguishing feature of all these attacks is the presence of abnormal forks, which means that our approach is also effective in reducing the extra profit made by attackers.
METHODS
Under the current protocol, Bitcoin maintains a block time of 10 min by measuring the growth of the main chain. If the growth becomes too slow, the network reduces the mining difficulty for the next period. A lower mining difficulty means that miners can find a block in a shorter time, including selfish attackers. Moreover, an attacker can trick the network into discarding others’ blocks by forking, which increases the proportion of its own blocks in the main chain. Thus, a low mining difficulty is an important precondition for an attack to be profitable. In other words, a selfish attack is not profitable if the mining difficulty is not adjusted. Therefore, keeping the mining difficulty stable is the key to deterring selfish attacks.
To analyze the influence of mining difficulty, we regard the difficulty adjustment period as a unit and calculate a miner’s profit in each unit. In our model, we consider a blockchain system with only two roles: the selfish miner pool and honest miners. Additionally, we introduce the mining cost in our model, which is not considered in the relative revenue model. Briefly, the unit model can be described as π(a,γ,ω,λ), and the physical implication of each parameter is as follows:
●→α ∈ [0, 0.5) is a selfish attacker’s hash power. It is also the probability of an attacker finding the next block. We normalize the total hash power of the network to 1, and because the honest miners are the rest of the network, their probability of finding the next block is 1-α.
●→γ ∈ [0,1] is the ratio of honest miners that are mining on the selfish attacker’s branch. Due to the network topology, each miner can extend only the branch that it initially listened to. This parameter is from Ref. 4 and an attacker cannot change it.
●→ω ∈ [0,1] is the mining cost of each share of the hash power. We simplify the complex mining cost as a coefficient that depends only on a miner’s hash power. This parameter can be regarded as the unit price of hash power.
●→λ ∈ [0,1] is the ratio of abandoned blocks that are recorded by honest miners. In our protocol, honest miners do not need to record all abandoned blocks. They can select a portion λ of such blocks to record.
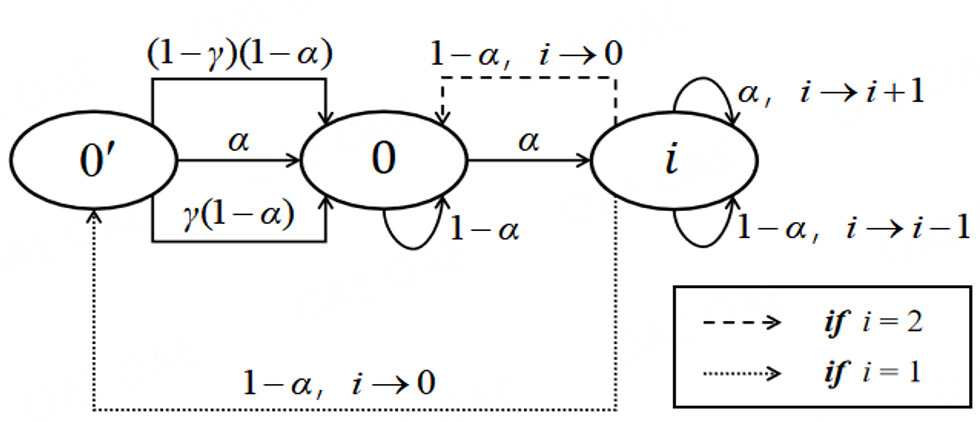
We show the progress of the selfish strategy as a state machine in Figure 1. The transition frequencies are the probability of a miner finding a block, where the attacker is α and the honest miner is 1-α. The number of a state is the difference between the number of blocks in the selfish attacker’s branch and in the main branch. There are 3 state in this machine: 0’ and i, where i represents the attacker’s lead greater than 0. For example, i=1 means the attacker’s branch has one block more than the other branch. When the lead is zero, there are two states, 0 and . State 0’ means the main chain has not forked, whereas state 0’ means the main chain has forked, but the two branches are the same length.
The aim of a selfish attack is to keep ahead of the other branch. If the lead is less than 2, the attacker will release its private branch and win the competition. That is, the attacker’s branch is competing with another branch to become the new main chain. There are three transitions from state 0’ to 0. Case I is that the attacker has found a new block and won, with probability α. Case II is that an honest miner has extended the attacker’s branch, with probability γ(1 - α). Case III is that another branch has won the competition, with probability(1-γ)(1-α).
Table 1 lists the state transitions and the number of blocks generated during a selfish-mining attack. It is an enhancement of the optimal selfish-mining model[17]. In this table, we use a 5-tuple (rp, ro, tp, to, ta) to represent the number of blocks generated. rp is the number of reward blocks earned by the selfish pool p in a unit, and ro is the same for the honest miners o. tp is the number of blocks mined by p in a unit, and to is the same for o. Finally, ta is the number of blocks from those branches that were published but abandoned by the main chain in a unit. We call these abandoned blocks. Note that all blocks need to be listened by the network, which means that hidden blocks are not included in (rp, ro, tp, to, ta). Unlike Eyal and Sirer’s model[4], our model also calculates tp, to, and ta to represent the number of blocks generated more completely. Their model considers a miner’s gain but ignores its loss from forking. Furthermore, we calculate these parameters in terms of unit adjustment periods, whereas their parameters are calculated for the whole mining process. This means that our model has finer granularity than their model and is more flexible. Additionally, the abandoned blocks represent the loss of effective hash power in the network, which is necessary when calculating mining difficulty correctly. Obviously, their model does not meet our requirements.
The first column in Table 1 is the current state of the network in a mining round and the attacker’s action in the next round. The state is described by a 3-tuple (a, h, fork), where α is the length of the attacker’s branch, h is the same but for the other branch, and fork takes three values: relevant, irrelevant, or active. Relevant means that the honest miners have published a block in this state and the attacker has a private branch in the previous state; thus, the attacker can release its branch. Irrelevant is the other way round. Active means that this state is forking. There are four actions for an attacker: adopt, override, match, and wait. Adopt means that the attacker has lost the forking competition and accepts the other branch. Override means that the attacker has released its private branch and won the competition. Match means that the attacker has released one block to the fork. Wait means that the attacker has skipped this round because it does not have any blocks. The second column is the next state, and the third column is the transition probability of the next state. For example, say, the current state is (a,h,∙), where α < h. This means that the attacker’s private branch is shorter than the honest branch. Thus, the current state is irrelevant to the next state. The attacker can perform only the adopt action in this state, but it can still aim to catch up with another branch. The probability of it finding a block is α. If it finds a block and holds it in the next mining round, the next state will be (1, 0, irrelevant). Briefly, the attacker is catching up with the honest miners, and it does not receive block rewards in this state. The block-generation tuple is (0, h, a, h, 0). Due to page limitations, we do not detail the other cases here, but the derivations are similar.
Transitions and block generation
| State × Action | Next State | Probability | Number of blocks generated1 |
| (a h,·),adopt | (1,0,irrelevant) | α | (0,h,a,h,0) |
| (0,1,irrelevant) | 1-α | ||
| (a,h,·),override2 | (a-h,0,irrelevant) | α | (h+1,0,h+1,h,h) |
| (a-h-1,1,relevant) | 1-α | ||
| (a,h,·),wait | (a+1,h,irrelevant) | α | (0,0,0,0,0) |
| (a,h+1,relevant) | 1-α | ||
| (a,h,active),wait (a,h,relevant),match3 | (a+1,h,active) | α | (0,0,0,0,0) |
| (a-h,1,relevant) | γ·(1-α) | (h,0,h,h,h) | |
| (a,h+1,relevant) | (1-γ)·(1-α) | (0,0,0,0,0) |
Unit profit of a miner with the current blockchain protocol
To improve the relative revenue model, we use the generalized unit profit function to evaluate a miner’s profit in each adjustment period. Let H* denote the probability of a new block being generated by miners * in a period, and D denote the mining difficulty of the current period. In each period, the aim of adjusting the mining difficulty is for ∑*(H*/D) → 1 in the next period, where the total block award expectation is normalized as 1, and H*/D is the unit profit of each miner *. This trend shows that the mining difficulty should accurately reflect the effective hash power of the network. However, the current protocol considers only the growth of the main chain in the previous period as a cursory estimate of the hash power of the network. If some blocks are abandoned due to a fork, the network will ignore the hash power used to generate them and will calculate the mining difficulty inaccurately. This drawback makes a selfish attack possible.
In our model, we consider that a miner’s unit profit is earned over two phases: the L phase, when a selfish attack is launched, and the ε phase, when the miner actually earns the unit profit. In the L phase, the profit expectations of both types of miner are as follows:
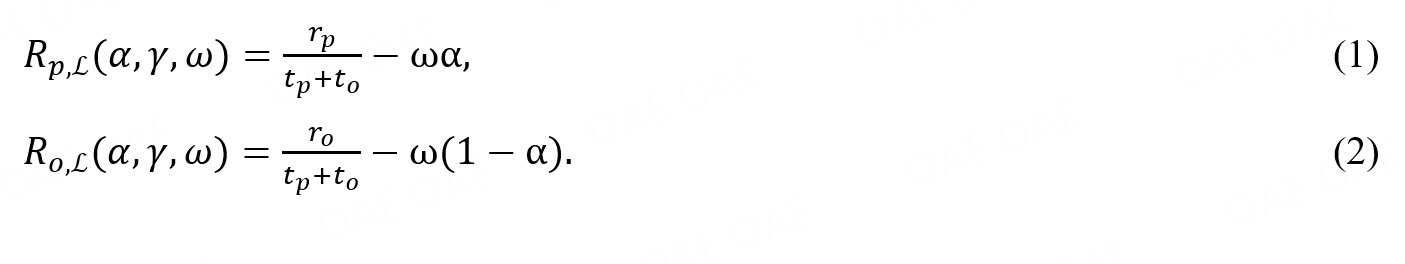
According to our definition of ω, the mining cost for an attacker is ωα, and for an honest miner, it is ω(1-α). In this phase, the mining difficulty is based on the number of blocks generated in the previous phase, which is approximately tp + to (i.e., there were no forks in the previous phase). Obviously, because rp ≤ tp and ro ≤ to , two inequalities always hold:
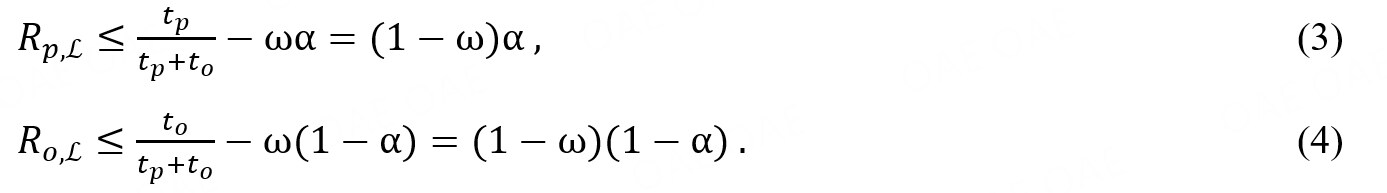
These inequalities show that both p and o receive a low profit in this phase, which means that the attacker’s profit will also drop in the short term until the mining difficulty decreases. In other words, a selfish attack is not immediately profitable.
In ε phase, the mining difficulty will be decreased from tp + to to rp + ro , since rp + ro is the effective growth of the main chain in the selfish launch phase. Thus, the unit profits in this phase are

These equations show that a sharp drop in mining difficulty will magnify the advantage of the selfish strategy. The attacker can increase its share of the hash power in the network by forking. Therefore, keeping the mining difficulty stable is an effective scheme for deterring selfish attacks.
Adaptive mining-difficulty adjustment protocol
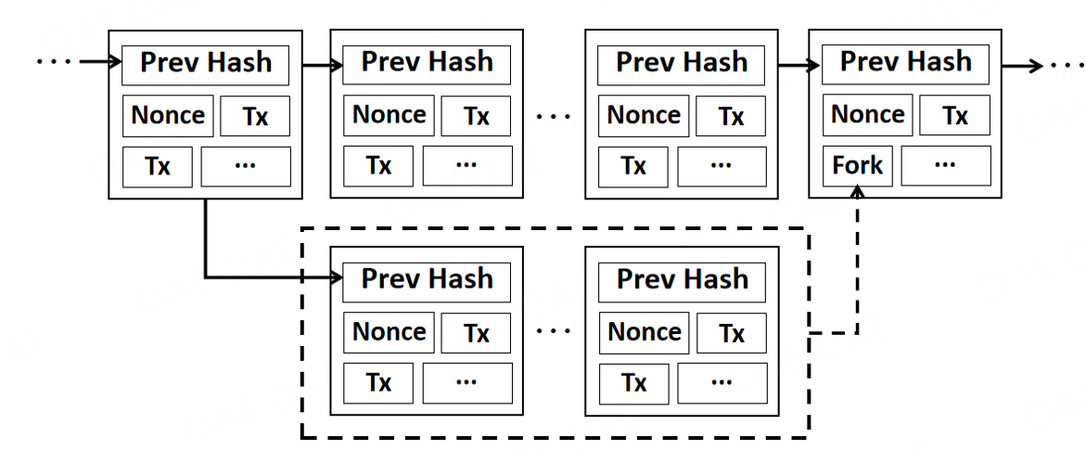
To ensure that the mining difficulty is stable, we designed a new approach, named the adaptive mining-difficulty adjustment protocol. Our protocol permits miners to record abandoned blocks as special transactions in the main chain, as shown in Figure 2. The pseudocode for our protocol is shown in Algorithm 1. In Bitcoin, nodes quickly validate a transaction by checking the Merkle root in the block header. A Merkle tree is a hash tree, such that its root is the hash of all tree nodes. Therefore, adding special transactions into leaf nodes does not actually increase the size of the block header or the storage pressure of the main chain, but full nodes do need to store the complete transaction history. Our protocol may increase the storage pressure for such nodes. Significantly, if an attacker gives up generating forks due to our protocol, then the number of abandoned blocks will greatly decrease, so that less storage space is needed. Therefore, our protocol should not affect the performance of the current blockchain, and its real-time performance is expected to be that achieved by Bitcoin. Furthermore, our protocol does not completely change the data structure of a block. Because of the adequate compatibility, we could use a soft fork to upgrade the protocol in the current network.
In our protocol Figure 3, the motivation for miners to record abandoned blocks is not to gain a direct reward but to protect their interests by deterring selfish attacks. Significantly, we define the λ to adjust the ratio of recorded fork blocks for controlling resource consumption. From the above discussion, rp+ ro is the increase in the length of the main chain and ta is the number of blocks abandoned in the last period. In brief, the current protocol takes the inaccurate effective hash power rp+ ro as the mining difficulty of the L phase. This is corrected in our protocol because it uses the hash power of the ignored branches λta. Therefore, following our protocol, the expected number of blocks generated in the ε phase is rp+ ro+λta. The profits of each miner in this phase are as follows:

Based on previous work[4], Table 2 gives the expected value for generating blocks in different cases. In this table, the first row is the number of blocks generated in each case, from a to h, as shown in Figure 4. Case a is when an attacker finds a block and maintains its private branch covertly. No blocks are published in the network. In case b, an honest miner finds a block in this round. The attacker releases its branch and gains two block rewards (rp = 2, tp =2). The honest miner abandons the block found (to = 1, ta = 1). In case c, an honest miner extends the attacker’s branch and helps the attacker win the competition. Thus, both p and o gain one block reward (rp = 1, tp =1, ro = 1, to = 2), but another branch is abandoned by the network (ta = 1). In case d, honest miners win the competition and gain two block rewards (ro = 2, to = 2), but the attacker’s block is abandoned (rp = 0, tp =1, ta = 1). Case e is when an honest miner finds and directly gains one block reward (ro = 1, to = 1), but the attacker does not have a private branch and skips this round (rp = 0, tp =0). Case f is when an honest miner finds a block and the attacker releases its hidden block, which is a precondition for cases c and d. Cases g and h are for when the attacker’s lead is more than 2. In case g, the lead of the attacker’s hidden branch drops to 1 because another branch has a new block. Thus, p publishes its hidden branch to win the competition and invalidate the other branch (rp = 2, tp =2, to = 1, ta = 1). In case h, an honest miner o finds a block, but the lead is still more than 2; thus, the attacker needs to release only the first hidden block to generate a fork. Note that this block can always bring one reward to p (rp = 1, tp =1), because a lead of more than 2 guarantees that the attacker defeats another branch (ro = 1, to = 1, ta = 1).
Original selfish mining revenue of each case
| Parameter | Case | |||||||
| a | b | c | d | e | f | g | h | |
| rp | 0 | 2 | 1 | 0 | 0 | 0 | 2 | 1 |
| ro | 0 | 0 | 1 | 2 | 1 | 0 | 0 | 0 |
| tp | 0 | 2 | 1 | 1 | 0 | 0 | 2 | 1 |
| to | 0 | 1 | 2 | 2 | 1 | 0 | 1 | 1 |
| ta | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| P case | (1 - p0’)a | p0’a | p0’·γ(1-α) | p0’ (1-γ)·(1-α) | p0(1-a) | P1(1-a) | P2(1-a) | P[i> 2](1-a) |
Figure 4. Block generation for each case a to h: state → state. The states are defined in Figure 1.
The final row in Table 2 for each case is the probability of the attacker’s state transition, where p0’, p0, p1, p2 and p[i > 2] are the probabilities for different leads. The expected values for t* and r* are as follows:

Where *∈{o,p}, C={a, b, c, d, e, f, g, h}, and Pcase is the probability of each case. In particular, t*,case, ta and r*,case represent the values of t*, ta and r* in each case, respectively. Values for p0’, p0, p1, p2 and p[i > 2] were calculated in a previous work[4], so we get:

Equations (7) and (8) show that our protocol can reduce a selfish attacker’s profit, but an honest miner would also get a lower reward if a selfish attack is launched, which may reduce the motivation of honest miners to record abandoned blocks. Unfortunately, previous research does not suggest intuitive and effective incentives for encouraging miners to record abandoned blocks. Thus, we consider setting a recording reward for honest miners. Let define the recording reward ratio, then we get:

Where λ is a function that is positively correlated with τ. Intuitively, the recording reward encourages honest miners to adopt our protocol. In contrast, recording fork blocks may reduce the selfish miner’s profit because a recording reward is much lower than a block reward, which implies that recording is not a wise option for an attacker. Due to page limitations, this issue is not discussed further in this paper.
Compared with the current protocol, our protocol reduces the growth rate of the main chain when a selfish miner is attacking. As a result, the transaction throughput of the blockchain is low, but this can be alleviated by increasing the amount of storage in each block to improve the transaction throughput per unit time. Moreover, when there is no attack, our protocol actually makes little impact on the growth rate of the main chain or the transaction throughput, because the probability of a natural fork is extremely low in a real network.
Security analysis of our protocol
In this section, we analyze the security of our protocol theoretically by modeling the repeated competition between an attacker p and another miner o using game theory. We define the adjustment period as each round of the game and use the unit profit to describe the miners’ payoffs in each round. Obviously, for each miner, the most important motivation of the mining strategy is to gain more profit. In our model, a selfish attacker can select either of two strategies: Honest (H) and Selfish (S). Similarly, an honest miner can choose to record (R) fork blocks or ignore (I) them. Thus, the mining game has the four scenarios listed in Table 3.
Miner game
| o | p | |
| H | S | |
| I | Rp(a,ω),Ro(a,ω) | Rp(a,γ,ω,0),Ro(a, γ,ω,0) |
| R | Rp(a,ω),Ro(a,ω) | Rp(a,γ,ω,λ),Ro(a, γ,ω,λ) |
The case (H, I) represents two miners who are following the current protocol. Their payoffs are:

The case (S, I) is when the attacker executes the selfish strategy, and its opponent does not record invalid blocks. In this case, the payoffs of the two miners are as follows:

Where rp, ro, tp and to can be calculated by Equations (1), (2), (5) and (6), respectively. Note that the final parameter λ = 0 indicates that the miners are not adaptively adjusting the mining difficulty.
The case (S, R) is when the honest miner follows the adaptive mining-difficulty adjustment protocol. Thus, the payoffs of the two miners in this case can be calculated by Equations (7) and (8).
Finally, the case (H, R) is when the honest miner records abandoned blocks and the attacker gives up following the selfish strategy. In this case, a natural fork is the only reason for blocks to be abandoned. However, the impact of natural forks on the network can generally be ignored as the probability is too low. Therefore, in this case, the miner’s payoff is approximately the same as for case (H, I).
Obviously, this repeated mining game is a non-cooperative game. Such a game is in a Nash equilibrium when each player’s strategy is optimal when considering the decisions of other players. In other words, each strategy in a Nash equilibrium is the best response to the other players’ strategies in that equilibrium[28]. Therefore, if (H, R) is a Nash equilibrium, then our protocol is effective and secure. Let α0 and α1 be two thresholds where α0 ≤ α1 and such that Rp,ε(α0,ω) = Rp,εα(0,λ,ω,0) and Rp,ε(α1,ω) = Rp,ε(α1,γ,ω,λ). The attacker can gain extra revenue when its hash power is larger than the threshold. Thus, we have the following three cases:
● (0 < α ≤ α0)In this case, the miners’ profits satisfy inequalities: Rp,ε(α,ω) ≥ Rp,ε(α,γ,ω,0)> Rp,ε(α,γ,ω,λ) and Ro,ε(α,γ,ω,0) > Ro,ε(α,γ,ω,λ). This means that an attacker does not have enough hash power to execute the selfish strategy, and the honest miner need not record the fork blocks. Thus, there is only one Nash equilibrium point (H, I).
● (α0< α≤ α1) We also have inequalities in this case: Rp,ε(α,γ,ω,0) > Rp,ε(α,ω) ≥ Rp,ε(α,γ,ω,λ) and Ro,ε(α,γ,ω,0) > Ro,ε(α,γ,ω,λ). In the current protocol, an honest miner’s interest will suffer if an attacker executes the selfish strategy. Therefore, an honest miner should raise the threshold for a selfish attack from α0 to α1 by adopting the adaptive difficulty adjustment-protocol. If the attacker’s hash power is less than α1, then the selfish strategy is the wrong option. This implies that there are two Nash equilibrium point: (S, I) and (H, R). Thus, the honest miner can adopt strategy R, with the aim of reaching the equilibrium point (H, R).
● (α1 < α ≤ 0.5) In this case, we similarly get: Rp,ε(α,γ,ω,0) > Rp,ε(α,γ,ω,λ) > Rp,ε(α,ω) and Ro,ε(α,γ,ω,0) > Ro,ε(α,γ,ω,λ). Importantly, there is only one equilibrium point (S, I) in this case. Thus, the attacker can execute the selfish strategy under the adaptive difficulty-adjustment protocol if α > α1, which is almost impossible to satisfy.
The above discussion shows that the case (H, R) is a Nash equilibrium in the mining game if α0 < α ≤ α1. This means that an attacker will degenerate into an honest miner if its hash power is less than the new threshold. Therefore, in theory, our protocol can effectively deter a selfish attack and enhance the security of the blockchain.
Significantly, the adaptive difficulty-adjustment protocol is valid for other attacks against the fairness of a blockchain. For example, in Nayak et al.’s[21] work, when a stubborn miner colludes with an eclipsed victim, the attacker’s gain can be given as:

Where α is the hash power of a stubborn miner, and λ is the hash power of honest miners. Our protocol can deter this type of attack as well, because gainC is proportional to selfishGain(α + λ), and selfishGain(α + λ)will decrease if the attacker’s hash power is smaller than α1. Unfortunately, our protocol is not completely effective against those attacks that combine selfish mining and BWH[27]. For example, an FAW attacker[19] divides its hash power into two parts, where one part is used to infiltrate other pools and the other part is used to mine honestly. Such an attacker uses the full PoW when mining in the infiltrated pool to generate a fork. This is a form of selfish attack, which our protocol can deter. However, the reward for an FAW attacker is always equal to or greater than that for a BWH attacker. Note that a BWH attack is always profitable[29], which means that our protocol can only reduce the reward for the FAW attacker but cannot defend against it.
Long-term profit analysis
Some attackers may prefer to gain extra profits in the short term, though they will gain a smaller long-term profit. In other words, these attackers do not have enough patience. In game theory, the discount factor represents the degree of patience of a player[30]. The lower the value, the less patient they are. Therefore, we introduce the discount factor to describe the future profit so that we can evaluate the long-term profit of miners who are eager to get block rewards. The long-term profit of miners can be calculated as follows:

Where β∈ (0, 1) denotes the discount factor and t is the round index. Let the long-term mining profits of a selfish attacker and an honest miner be

where α denotes the hash power of a selfish miner. Thus, the four scenarios for a mining game with long-term profits are listed in Table 4 Similarly, the long-term mining game has three cases, as considered in our. However, the values of α0 and α1 will be different, as they depend on the discount factor β. We give a detailed analysis of the various situations in the next section.
Mining game with long-term profit
| o | p | |
| H | S | |
| I | (αβ)/(1-β), (1-α)β/(1-β) | Rp,L(a,γ,ω,0)+ (β)/(1-β) Rp,ε(a,γ,ω,0), Ro,L(a,γ,ω,0)+ (β)/(1-β) Ro,ε(a,γ,ω,0) |
| R | (αβ)/(1-β), (1-α)β/(1-β) | Rp,L(a,γ,ω, λ)+ (β)/(1-β) Rp,ε(a,γ,ω, λ), Ro,L(a,γ,ω, λ)+ (β)/(1-β) Ro,ε(a,γ,ω, λ) |
RESULTS
To validate our theoretical analysis, we use the Bitcoin protocol simulator developed by Carlsten et al.[20] to simulate a selfish attack. In the simulator, the block arrival time in each mining round is exponentially distributed with an expected value of 600. There are only two miners, who execute a selfish strategy and an honest strategy, respectively. We varied the attacker’s hash power α in the range with as the step size. For each value of, we ran the simulation 10 times and averaged the results. Each simulation run generated 3,000 blocks. The simulation results and the theoretical results are summarized as follows.
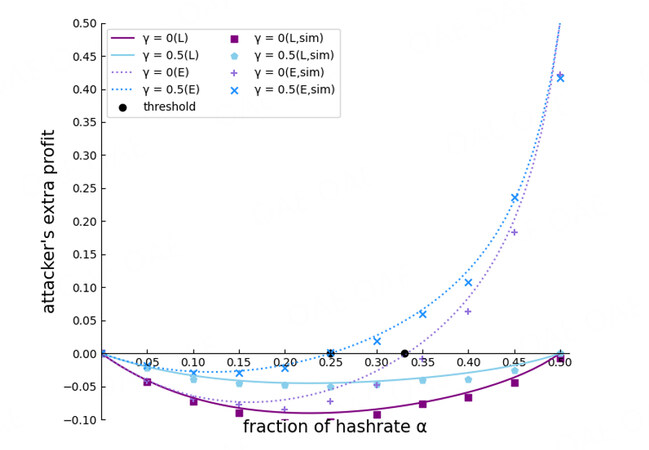
Result 1: Under the current protocol, the selfish attacker loses some profit in the Lphase, but after the difficulty is adjusted, an attack is profitable if the attacker’s hash power exceeds the attack threshold. The attack threshold is inversely proportional to γ.
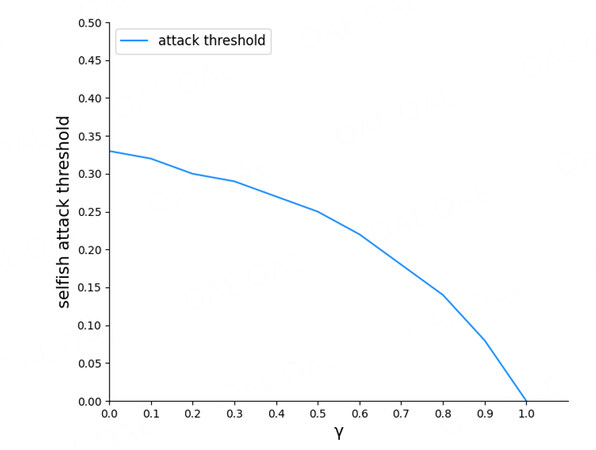
We compare the extra profit of the attacker in different phases, as shown Figure. 5. The extra profit is the profit difference between the selfish strategy and the honest strategy. The extra profit is greater than 0 if the selfish strategy is more profitable than the honest strategy; otherwise, it is less than 0. In Figure 5, solid lines (L) and dotted lines (E) represent the L phase and the ε phase, respectively. All the solid lines are below 0, whatever is. Thus, the attacker cannot gain extra profit, but also it makes a negative extra profit. In contrast, the dotted lines are above 0 when α is greater than the attack threshold. Briefly, the selfish strategy lowers the attacker’s profit in the L phase. If the mining difficulty is low, the attacker gains more profit than if it follows the protocol. Figure 6 shows that γ is inversely proportional to the attack threshold. A larger γ means that the attacker’s branch gathers more honest hash power, which increases the attacker’s chances of winning. In particular, the attack threshold is 0 when γ is 1, but this is impossible in reality.
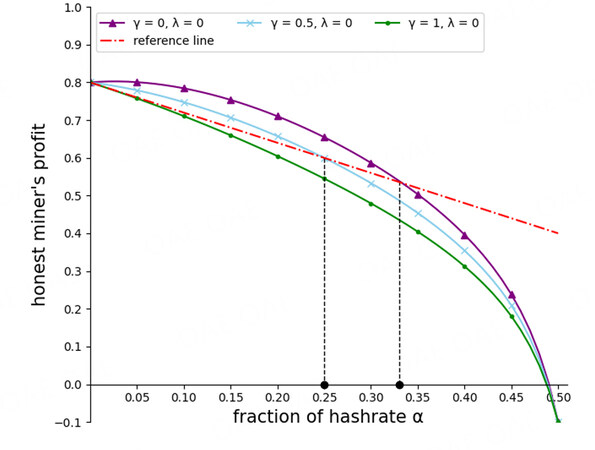
Result 2: If the attacker’s hash power does not exceed the attack threshold, then executing the selfish strategy will allow an honest miner to gain extra profit. In contrast, if the attacker has enough hash power, a selfish attack will threaten the other miners’ interests. Therefore, miners can adopt our protocol to deter a selfish attack, because our protocol can effectively raise the attack threshold.
Figure 7 illustrates the honest miner’s profit with different γ in the current protocol (λ = 0). Note that we present its profits for only the L phase, because a selfish attack is profitable in this phase only. The solid lines represent the miner’s profit. The red dashed-dotted line is a reference and represents the honest miner’s profit if there were no selfish attacks. In the area below this line, honest miners lose some profit due to the attack. The solid lines are higher than the reference line when the attacker’s hash power is less than the attack threshold. In this case, the attack allows the honest miner to gain extra profit. However, when the attacker’s hash power is greater than the threshold, the attack reduces the honest miner’s profit. Therefore, a higher attack threshold can protect the honest miner’s interests.
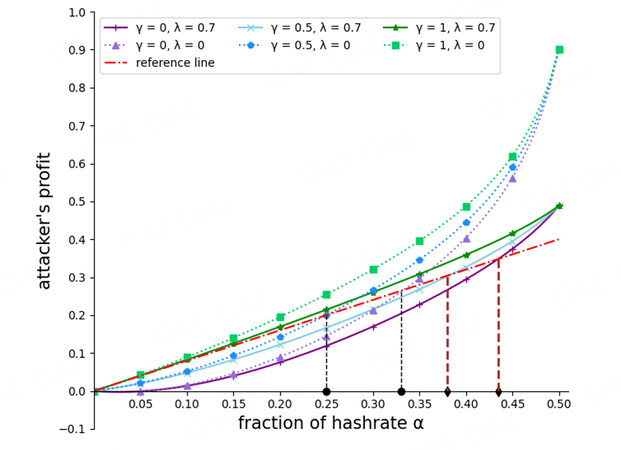
Figure 8 shows the attacker’s profit for different protocols. We analyze the L phase only. The solid lines represent the attacker’s profit for our protocol, and the dotted lines show it for the current protocol. The dashed lines mark the attack threshold for the different protocols. The brown lines are for our protocol, corresponding to α1, whereas the black lines correspond to α0. Obviously, both the brown lines are to the right of the black lines, which means that our protocol can effectively raise the selfish attack threshold. For example, when γ = 0.5 and λ = 0.7, the attack threshold in the current protocol is about 0.25, but in our protocol, it has increased to about 0.37, that is, by about 30%. Therefore, the attacker may give up the selfish strategy if the honest miner records abandoned blocks. In summary, the game transfers from (S, I) to (S, R), and then from(S, R) to (H, R).
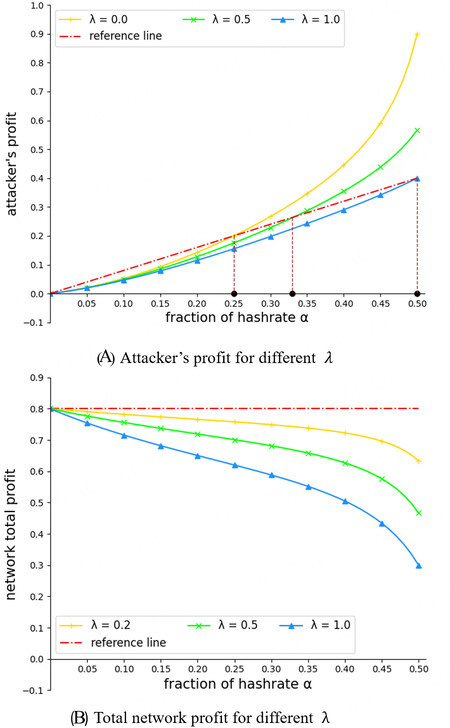
Result 3: The attack threshold is proportional to λ. Thus, the larger λ is the higher the attack threshold. However, if the attacker still attacks in our model, recording abandoned blocks would decrease the total profit of the network. The larger λ is, the lower the total network profit.
Figure 9 illustrates the impact of λ on the attack threshold and on the total network profit when the attacker executes a selfish strategy with γ =0.5 and ω = 0.2. The total network profit is the sum of the two miners’ profits. Figure 9(A) is the attacker’s profit for different λ. The attack threshold is proportional to λ, so that the larger λ is, the higher the threshold. Figure 9(B) illustrates the total network profit with different λ, with the attacker still executing the selfish strategy. The red dashed-dotted line is a reference line, which represents the total network profit without an attack (ta = 0). For lines below the reference line, the total network profit does not meet the expectation. All the solid lines are below the reference line. The greater λ is, the lower the total network profit. A larger λ causes the total network profit to decrease if the attacker still generates forks. Our protocol corrects the mining difficulty, but forks are still generated. In this case, increasing the mining difficulty slows down the growth of the main chain, which is bad for all miners. In other words, (S, R) is the worst gaming case for all miners.
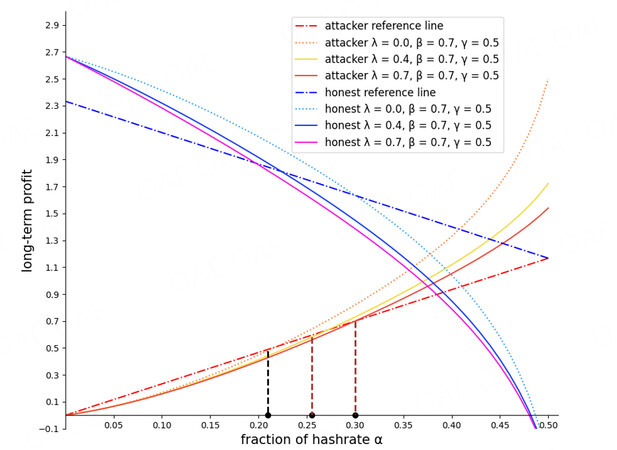
Result 4: The attacker may become more aggressive in forking to gain more long-term profit. Fortunately, our protocol also effectively raises the attack threshold in the long-term profit model. The attack threshold is proportional to β. The mining cost also affects the threshold in the long-term profit model: the larger ω.
Figure 10 illustrates the two miners’ long-term profits for different protocols. Dotted lines represent the profit under the current protocol (λ = 0), whereas solid lines represent it under our protocol (λ > 0). The red dashed-dotted line is the reference line for a selfish attacker, corresponding to Equation (25). The blue dashed-dotted line is for the honest miner, corresponding to Equation (26). We used different colored dashed lines to mark the attack threshold in the different protocols. Brown lines represent our protocol. In this figure, the brown lines are to the right of the black line, which proves that our protocol is also effective in the long-term profit model. However, the attack thresholds in this model are lower than in the unit profit model. For example, in Figure 8 , the attack threshold is approximately 0.44 (γ = 0.5, λ = 0.7, ω = 0.2), but in Figure 10 , it is about 0.3 (γ= 0.5, λ = 0.7, β = 0.7, ω = 0.2). This means that the attacker may be more likely to execute a selfish strategy to gain more future profit.
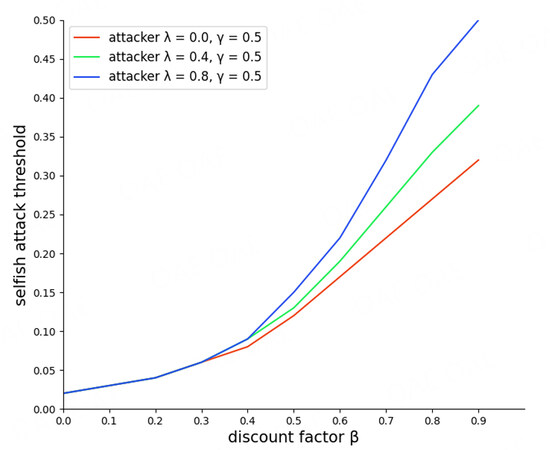
Figure 11 shows the attack threshold for different β to illustrate the correlation between the attack threshold and the attacker’s patience. Obviously, the attack threshold is proportional toβ, so that the larger β is, the higher the threshold. Thus, if the attacker wants to maintain a selfish attack under our protocol, corresponding to the case (S, R), it must invest a huge amount of hash power to avoid losses. Furthermore, the larger λ can further increase the costs of the attacker’s patience. In other words, the attack becomes quite passive in the repeated game when the other miner starts recording abandoned blocks, and giving up the attack becomes a more reasonable option.
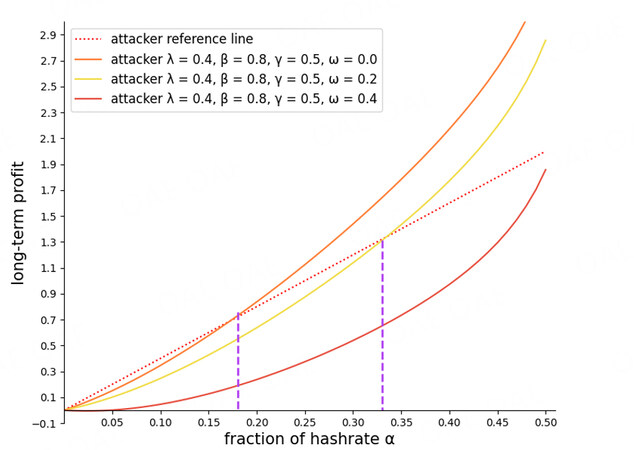
Figure 12 illustrates the attacker’s long-term profit with different ω. A larger ω leads to a higher attack threshold. The mining costs increasingly become a huge risk for the attacker as the game proceeds. Increasing ω increases the mining costs in each round, which further suppresses a selfish attack.
CONCLUSIONS
In this paper, we revisited the selfish strategy and proposed an adaptive mining-difficulty adjustment protocol to deter selfish mining. First, we described the shortcomings of the relative revenue model and proposed our unit profit model for estimating miners’ profits more accurately. Compared to the relative revenue model, we use the adjustment period for mining difficulty as a unit, because the selfish strategy only becomes profitable when the difficulty is adjusted. Significantly, this approach allows us to analyze a repeated mining game and derive possible outcomes of the competition.
Second, we proposed the adaptive mining-difficulty adjustment protocol as an enhancement of the current protocol. It can evaluate the effective hash power of the network more accurately and ensure that the mining difficulty is more stable. However, result 3 shows that, with our protocol, recording abandoned blocks would lower the profit for all types of miners when an attack is launched, which may reduce the incentive for miners to adopt our protocol. Our new protocol is a preliminary solution for deterring a selfish attack; however, it still needs further improvement. Thus, we leave this as future work.
Finally, our simulation results show that our protocol can raise the threshold for the selfish strategy, so that an attacker may actively degenerate into an honest miner during a repeated competition. The increase of the threshold is proportional to λ, and the new threshold is about larger 30% than the old one when λ = 0.7 and γ = 0.5. Briefly, our approach can alleviate the abnormal fluctuations in the mining difficulty, making the expected block time and network throughput more stable. Importantly, the protocol can effectively protect honest miners’ interests and establish a more stable and fairer mining game for the blockchain.
DECLARATIONS
AcknowledgmentsThe authors thank the reviewers and editor for their invaluable comments.
Authors’ contributionsMade substantial contributions to the conception and design of the study and performed data analysis and interpretation: Wang J, Wu S, Liang H, Ding Y, Zhai Y
Availability of data and materialsNot applicable.
Financial support and sponsorshipThis work is supported in part by the National Key R&D Program of China under project 2020YFB1006003, the National Natural Science Foundation of China under project 6217070229, the Guangdong Key R&D Program under project 2020B0101090002, the Open Program of Guangxi Key Laboratory of Cryptography and Information Security under Grant GCIS202126, and the Innovation Project of GUET Graduate Education under project 2022YCXS073.
Conflicts of interestAll authors declared that there are no conflicts of interest.
Ethical approval and consent to participateNot applicable.
Consent for publicationNot applicable.
Copyright© The Author(s) 2023.
REFERENCES
1. Nakamoto S. Bitcoin: A peer-to-peer electronic cash system. Available from: https://bitcoin.org/bitcoin.pdf [Last accessed on 5 May 2023].
2. Li C, Wang L, Yang H. The optimal asset trading settlement based on proof-of-stake blockchains. Decision Support Systems 2023;166:113909.
3. Liu Y, Xu G. Fixed degree of decentralization DPoS consensus mechanism in blockchain based on adjacency vote and the average fuzziness of vague value. Computer Networks 2021;199:108432.
4. Ittay Eyal, Emin G. Sirer. Majority is not enough: Bitcoin mining is vulnerable. Communications of the ACM 2018;61(7): 95-102.
5. Yoko S, Go Y, Fuhito K, et al. Selfish mining attacks exacerbated by elastic hash supply. Financial Cryptography and Data Security 2021;12675:269-276.
6. Nigam S, Sugandh U, Khari M, et al. Chapter eighteen - the integration of blockchain and IoT edge devices for smart agriculture: Challenges and use cases. Adv. Computer 2022;27:507-37.
7. Rupa C, Jaya Kumari D, Gadekallu TR, Iwendi C. Distributed-ledger-based blockchain technology for reliable electronic voting system with statistical analysis. Electronics 2022;11:3308.
8. Chen H, Chi P, Chuang Y. Building a privacy-preserving blockchain-based bidding system: a crypto approach. IEEE Access 2022;10:13367-78.
9. Jingjing Z, Yingyao R, Jiannong C, et al. DBFT: a byzantine fault tolerant protocol with graceful performance degradation. 38th symposium on reliable distributed systems, SRDS 2019 Oct. 1-4; Lyon, france.
10. Bentov I, Lee C, Mizrahi A, Rosenfeld M. Proof of activity: extending Bitcoin's Proof of work via proof of stake [Extended Abstract]y. SIGMETRICS Perform Eval Rev 2014;42:34-7.
11. Castro M, Liskov B. Practical byzantine fault tolerance and proactive recovery. ACM Trans Comput Syst 2002;20:398-461.
12. Kostis K, Aggelos K, Dionysis Z. Proof-of-burn. Financial Cryptography and Data Security 2020; 12059:523-540.
13. Pass R, Shi E. FruitChains: a fair blockchain. Proceedings of the ACM symposium on principles of distributed computing, PODC; 2017 July 25-27; Washington, DC, USA, 2017.
14. Chen F and Jianyu N. Selfish mining in ethereum. IEEE international conference on distributed computing systems of the 35th, ICDCS 2019 july 7-10. Dallas, TX, USA, 2019
15. Kang H, Chang X, Yang R, Misic J, Misic VB. Understanding selfish mining in imperfect bitcoin and ethereum networks with extended forks. IEEE Trans Netw Serv Manage 2021;18:3079-91.
16. Wang Y, Wang Z, Zhao M, et al. BSM-ether: bribery selfish mining in blockchain-based healthcare systems. Information Sciences 2022;601:1-17.
17. Sapirshtein A, Sompolinsky Y, Zohar A. Optimal selfish mining strategies in bitcoin. Financial cryptography and data security 2016; 9603:515-32.
18. Hanqing L, Na R, Rongtian D, Weijia J. On the strategy and behavior of bitcoin mining with n-attackers. Proceedings of the 2018 on asia conference on computer and communications security, AsiaCCS 2018 june 04-08; Incheon, republic of korea,
19. Kwon Y, Kim D, Son Y, Vasserman E. Be selfish and avoid dilemmas: fork after withholding (FAW) attacks on bitcoin. Proceedings of the 2017 ACM SIGSAC conference on computer and communications security, CCS 2017 Oct. 195-209; Dallas, TX, USA,
20. Carlsten M, Kalodner H, Weinberg SM, Narayanan A. On the instability of bitcoin without the block reward. Proceedings of the 2016 ACM SIGSAC conference on computer and communications security; 2016 Oct. 24-28; Vienna, austria.
21. Nayak K, Kumar S, Miller A, Shi E. Stubborn mining: generalizing selfish mining and combining with an eclipse attack. IEEE european symposium on security and privacy, EuroS&p; 2016 March 21-24; Saarbrücken, germany;
22. Decker C, Wattenhofer R. Information propagation in the bitcoin network. IEEE international conference on peer-to-peer computing of the 13th, 2013 Sept 9-11; Trento, italy.
23. Gervais A, Ritzdorf H, Karame GO, Capkun S. Tampering with the delivery of blocks and transactions in bitcoin. Proceedings of the 22nd ACM SIGSAC conference on computer and communications security 2015 Oct, 12-16; Denver, CO, USA.
24. Qianlan B, Xinyan Z, Xing W, et al. A deep dive into blockchain selfish mining. IEEE international conference on communications, ICC; 2019 May 20-24; Shanghai, china.
25. Na R, L Han-Qing, S Xue-Ming. Catfish effect between selfish miners in proof-of-work based blockchain. Chinese Journal of Computers 2012; 44(1):16.
26. Marmolejo-Cossío FJ, Brigham E, Sela B, Katz J. Competing (semi-)selfish miners in bitcoin. Proceedings of the 1st ACM conference on advances in financial technologies; 2019 october 21-23; Zurich, switzerland.
27. Dong X, Wu F, Faree A, Guo D, Shen Y, Ma J. Selfholding: a combined attack model using selfish mining with block withholding attack. Computers & Security 2019;87:101584.
28. Amir R, De Castro L. Nash equilibrium in games with quasi-monotonic best-responses. JET 2017;172:220-46.
29. Bag S, Ruj S, Sakurai K. Bitcoin block withholding attack: analysis and mitigation. IEEE Trans Inform Forensic Secur 2017;12:1967-78.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Wang J, Wu S, Liang H, Ding Y, Zhai Y. Adaptive mining difficulty for blockchain to resist selfish mining attack. J Surveill Secur Saf 2023;4:14-34. http://dx.doi.org/10.20517/jsss.2023.05
AMA Style
Wang J, Wu S, Liang H, Ding Y, Zhai Y. Adaptive mining difficulty for blockchain to resist selfish mining attack. Journal of Surveillance, Security and Safety. 2023; 4(2): 14-34. http://dx.doi.org/10.20517/jsss.2023.05
Chicago/Turabian Style
Wang, Jing, Senkai Wu, Hai Liang, Yong Ding, Yong Zhai. 2023. "Adaptive mining difficulty for blockchain to resist selfish mining attack" Journal of Surveillance, Security and Safety. 4, no.2: 14-34. http://dx.doi.org/10.20517/jsss.2023.05
ACS Style
Wang, J.; Wu S.; Liang H.; Ding Y.; Zhai Y. Adaptive mining difficulty for blockchain to resist selfish mining attack. J. Surveill. Secur. Saf. 2023, 4, 14-34. http://dx.doi.org/10.20517/jsss.2023.05
About This Article
Special Issue
Copyright
Data & Comments
Data

 Cite This Article 4 clicks
Cite This Article 4 clicks













Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.