Evaluating the performance of post-quantum secure algorithms in the TLS protocol

1. INTRODUCTION

Cryptography is a main information security mechanism, providing services to achieve several security goals such as confidentiality, data and entity authentication, and non-repudiation; however, it actually goes far beyond these goals and is able to provide solutions in terms of fulfilling legal requirements with respect to personal data protection and privacy ^[1]. To this end, cryptographic algorithms constitute core elements in network security protocols, including the prominent transport layer security (TLS) protocol ^[2], which constitutes a somewhat de facto standard for web security ^[3]. Indeed, TLS ensures: (i) entity authentication through digital certificates that are digitally signed (via a public key digital signature algorithm) by trusted certification authorities; (ii) confidentiality through encrypting (via the use of symmetric ciphers) the content of the communications, while the symmetric key for encryption/decryption is being securely exchanged via public key (i.e., asymmetric) cryptographic techniques; and (iii) data integrity, via ensuring that the encryption is authenticated (via message authentication codes or suitable modes of operations allowing for authenticated encryption). Any weakness in cryptographic algorithms affects the overall security of the protocol (see, e.g., ^[4] for a survey on such cryptographic threats for TLS).

The imminent advent of quantum computers will highly change the situation with regard to which cryptographic algorithms should be considered secure. Indeed, having large-scale quantum computers will allow executing algorithms that can efficiently solve difficult problems that cannot be solved today by contemporary conventional computing systems. More precisely, due to a quantum algorithm proposed by Peter Shor in 1994 ^[5], all commonly used public-key systems (including RSA, elliptic curve cryptography, and the Diffie–Hellman algorithm that is being used in the TLS protocol) will no longer be secure. Symmetric cryptography is also affected, but not to the same extent: there is a known quantum algorithm developed by Grover in 1996 ^[6] that suffices to decrease the security level of symmetric algorithms by up to half, which means that contemporary symmetric cryptographic primitives may still provide security to the post-quantum era by doubling, if needed, the key sizes (for symmetric ciphers) or the sizes of the message digests (for cryptographic hash functions).

Post-quantum cryptography refers to cryptographic algorithms which are secure under the assumption that the attacker has a quantum computer. Although the quantum computers that (are known to) exist currently are not large enough to violate the security of contemporary cryptography, it is essential to start considering the implementation of post-quantum cryptographic algorithms. The basic idea is to develop public-key algorithms whose security relies on a difficult mathematical problem that will remain difficult even if large-scale quantum computers become a reality. Hence, the US National Institute of Standards and Technology (NIST) launched in 2017 a process to standardize one or more quantum-resistant public-key cryptographic algorithms by collecting and evaluating submissions from the cryptographic community around the world ^[7]. This evaluation process is still ongoing, being in its third round of evaluation when the present research was conducted (and since July 2022, during the review phase of this paper, a fourth round has been initiated). The NIST process aims to find post-quantum secure public key algorithms that can be used either for digital signatures or to provide confidentiality, which in turn also incorporate secure key exchange (KEX) techniques as well as key encapsulation mechanisms (KEMs).

NIST evaluates the security strength of post-quantum secure algorithms on the basis of five categories which are characterized in terms of the equivalent strength of a symmetric primitive. In particular, according to NIST, a separate category for each of the following security requirements is defined (from the lowest strength to the highest strength):

● Level $$ 1 $$ (L1): Any attack that breaks the relevant security definition must require computational resources comparable to or greater than those required for key search on a block cipher with a $$ 128 $$-bit key (e.g., AES128).

● Level $$ 2 $$ (L2): Any attack that breaks the relevant security definition must require computational resources comparable to or greater than those required for collision search on a $$ 256 $$-bit hash function (e.g., SHA256/SHA3-256).

● Level $$ 3 $$ (L3): Any attack that breaks the relevant security definition must require computational resources comparable to or greater than those required for key search on a block cipher with a $$ 192 $$-bit key (e.g., AES192).

● Level $$ 4 $$ (L4): Any attack that breaks the relevant security definition must require computational resources comparable to or greater than those required for collision search on a $$ 384 $$-bit hash function (e.g., SHA384/SHA3-384).

● Level $$ 5 $$ (L5): Any attack that breaks the relevant security definition must require computational resources comparable to or greater than those required for key search on a block cipher with a 256-bit key (e.g., AES 256).

Currently, the NIST competition is in the fourth round, as subsequently described.

During these years, the research community has also started exploring whether known public-key post-quantum secure cryptographic algorithms can be implemented in contemporary systems to enrich current security protocols by post-quantum secure ciphers. The actual motivation is that it is essential to start deploying quantum-safe solutions even before large-scale quantum computers become available. This is nicely explained by the famous Mosca equation (see, e.g., ^[8]): if $$ x $$ denotes how long we need our cryptographic keys to be to remain secure, $$ y $$ denotes how long it will take to deploy a set of tools that are quantum-safe (i.e., the migration time), and $$ z $$ denotes the so-called collapsed time, i.e. the time needed to have a quantum computer, or some other method, that will break the currently deployed public-key cryptographic algorithms, then we have a serious problem if $$ x+y > z $$. Moreover, with respect to the time $$ z $$, Mosca estimated since $$ 2015 $$^[8] that there is a $$ 1/7 $$ chance of breaking RSA-$$ 2048 $$ by $$ 2026 $$ and a $$ 1/2 $$ chance by $$ 2031 $$. Therefore, incorporating post-quantum ciphers in the TLS protocol is currently a significant research field (see, e.g., ^[9–14]).

This paper focuses on the embedding of post-quantum secure cryptographic algorithms into the TLS protocol. More precisely, in this study, we performed a comprehensive set of experiments towards examining all possible post-quantum cryptographic algorithms for key exchange that are being analyzed by NIST, in terms of how efficiently they can be implemented into the TLS 1.3 protocol. More precisely, we studied all the finalists of the third round of the NIST competition, which was ongoing when this research was conducted. For our experiments, we used combinations of cloud and local virtual machines per case. The implementations of the algorithms were based on the Open Quantum Safe project ^[15] and our experiments constituted a more extended set of experiments with respect to those presented in ^[10], which formed the main basis for our research. Our ultimate goal was to derive conclusions on whether the transition to post-quantum secure algorithms will have a significant impact on the user experience due to the possible increase of client–server handshake communication times, for various network types that are being investigated — and this for each possible post-quantum secure cipher. Our results confirm that, in terms of performance, there are some very promising algorithms that could be utilized in the near future.

The paper is organized as follows. The basic background, with respect to both post-quantum cryptography and the TLS protocol, is given in Section $$ 2 $$. A presentation of relative previous work in the field is given in Section $$ 3 $$. The description of how the experimental environment was set up, based on previous relevant works, is given in Section $$ 4 $$, along with a discussion on the motivation for these experiments and their added value compared to previous works, whereas the results of our experiments are presented in Section $$ 5 $$. A discussion on the results, stating the main conclusions derived, is given in Section $$ 6 $$. Finally, concluding remarks and suggestions for future research steps are given in Section $$ 7 $$.

2. BACKGROUND

3. RELEVANT PREVIOUS WORK

Embedding post-quantum secure ciphers in the TLS protocol has already been studied by many researchers, due to its high importance. Our research heavily relied on the work presented in ^[10], which presents a framework for running relevant experiments in TLS by emulating network conditions; more precisely, the testbed developed therein allows controlling variables such as link latency and packet loss rate, and then examining the performance impact of various post-quantum ciphers, both for key establishment and for digital signatures, based on the implementations from the Open Quantum Safe project ^[15]. As illustrated by the work in ^[10], the network latency hides most of the impact from algorithms with slow performance, while, for some of the algorithms studied therein, a packet loss rate above 3–5% seems to have an impact on the performance.

In ^[12], an assessment, through relative experiments, of the concurrent use of quantum-resistant key exchange and authentication in TLS 1.3, as well as SSH protocols, under realistic network conditions, is carried out. It is shown that there exist combinations of algorithms that offer handshake performance close to the current standards (a minimum slowdown of about $$ 1 $$% has been monitored). It is interesting to point out that these "nice" combinations include the lattice-based Kyber cipher, which has been subsequently selected by NIST as the first post-quantum secure standard for public key encryption and KEM. A similar approach is also followed in ^[13] but for post-quantum digital signature algorithms. The performance of post-quantum digital signature algorithms is also studied in ^[20], and a security comparison of these algorithms is also performed therein.

In parallel with our work, a nice study on the performance of the TLS based on post-quantum secure algorithms is presented in ^[21]; this work utilizes the liboqs software library ^[22] that was also used in our experiments, as subsequently described. A main outcome of this work is that Saber or CRYSTALS-KYBER for key exchange together with the FALCON signature seems to be a right combination for achieving the best performance, while in general lattice-based cryptography can be compared to RSA and elliptic curve cryptography, outperforming these classical schemes at higher security levels. The work in ^[21], however, does not take into account network parameters.

Another relative work in the field is found in ^[14], which focuses explicitly on the Google-Cloudflare CECPQ2 experiment for integrating post-quantum key-exchange algorithm into TLS 1.3 for developing a solution achieving higher performance; however, since this experiment utilizes a variant of one of the algorithms in the NTRU proposal, the proposed solution is also based on NTRU. Finally, an integration of the post-quantum KEM scheme Kyber for key establishment and the post-quantum signature scheme SPHINCS+ into the embedded TLS library (mbed TLS) is presented in ^[11], illustrating that embedded systems can (at least) act as post-quantum secure TLS clients, for those studied algorithms.

4. THE TESTING ENVIRONMENT

This section describes the experiments that were carried out to evaluate the performance of TLS $$ 1.3 $$ (under several configuration parameters) if its public key algorithms for symmetric key exchange are being replaced by post-quantum secure ciphers — namely, by the finalists in the third round of the NIST evaluation process.

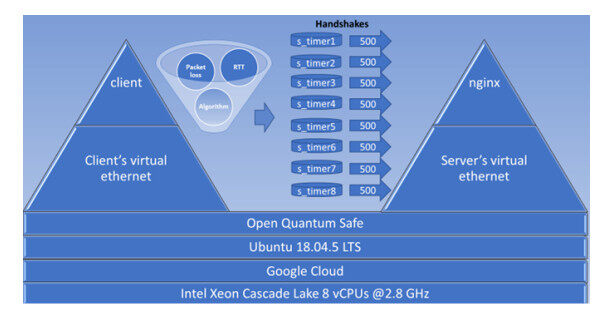
The testing environment consisted of one Google cloud device (Intel Xeon Cascade Lake n2-custom, with $$ 8 $$ vCPUs and $$ 16 $$ GB memory at $$ 2.8 $$ GHz) and two local devices, being executed as virtual devices through the Oracle Virtual Box (version $$ 6.1 $$). The first one was running over a desktop PC with Intel Core i-$$ 7 $$$$ 6700 $$k at $$ 4 $$ GHz, whereas the second was running over a laptop with Intel Core i5-$$ 8250 $$U at $$ 1.6G $$Hz. Each virtual device was assigned with $$ 2 $$ Gb memory and a single-core processor. For all virtual devices (i.e., the two local devices and the cloud device), the operating system was Ubuntu $$ 18.04.5 $$ LTS (Bionic Beaver). All processors made use of Advanced Vector Extensions 2 (AVX2), an extension of AVX, which was first introduced in Intel Haswell family of processors; this is an important feature since many of the algorithms that were being studied in this experiment take advantage of this technology to improve their efficiency. It should be pointed out that the utilization of processors with varying processing capabilities allowed conducting experiments to see how the processor power affects the performance of post-quantum TLS.

To implement simulations that resemble realistic scenarios with regard to client–server connections, Linux network namespaces were used with the aim to develop different network entities, which in turn can be interconnected through virtual Ethernet. A network emulator was used to perform experiments for several probabilities of packet loss and for several round-trip times (RTTs).

The experiments are based on the following:

1. On a fork of the pq-tls-benchmark ^[23] which contains code and associated data for benchmarking post-quantum cryptography in TLS $$ 1.3 $$, appropriately adapted to fit our context; this fork constitutes a companion to the work presented in ^[10], which forms the basis for our work.

2. On liboqs, an open source C library for quantum-resistant cryptographic algorithms from the Open Quantum Safe (OQS) Project ^[15], which provides an open-source implementation of the post-quantum secure algorithms for the TLS $$ 1.3 $$, either from the PQClean project or directly from their submissions to the NIST. This library is available for research purposes.

More precisely, the aforementioned fork was used for the first two types of experiments, while for the third experiment, we used liboqs ^[22].

Our experiments included all the post-quantum secure ciphers for key exchange that were analyzed in the third round of the NIST evaluation procedure for all possible security levels; an exemption was the McEliece cipher for the first two experiments due to the large delay that occurred. Indeed, the McEliece cipher, as stated in the NIST Status Report on the Second Round of the Post-Quantum Cryptography Standardization Process ^[24], has a very large public key and, thus, does not fit well with Internet protocols as they are currently specified (although it is still an appealing choice for standardization, since it achieves the smallest ciphertext among alls KEMs and, thus, is preferable for some applications). We also examined hybrid versions of these ciphers — i.e., being combined with a classic elliptic curve cipher. Such versions are provided by the OQS project, such as, if quantum-safe public-key algorithms are used in conjunction with traditional public key algorithms, the derived implementation is at least no less secure than existing traditional cryptography^[15]. More information on hybrid implementation for key exchange in TLS $$ 1.3 $$ can be bound in ^[10].

The ciphers (for the key exchange) examined for the first two experiments, which utilize simulation of TLS connections, are shown in Table 1. Each cipher has several versions depending on its parameters to achieve a specific security level according to the NIST requirements; as it can be seen, a classical elliptic curve (EC) algorithm for key exchange was also considered — namely, the elliptic curve Diffie–Hellman (ECDH) algorithm, with the NIST Curve P-$$ 256 $$.

In all cases, the most recent version, TLS 1.3, of the protocol was used, whereas the data exchanged were encrypted by AES-256 GCM (Galois/Counter Mode). The server's authentication was based on the ECDSA certificate, signed with ECDSA P-$$ 256 $$ with SHA-$$ 384 $$.

We also executed a third experiment focusing explicitly on the post-quantum algorithms without incorporating them into a TLS implementation. In this experiment, the McEliece variants were also taken into account.

5. RESULTS

This sections presents the results from our range of experiments that took place.

5.1. First experiment: Analysis for several network parameters

The first experiment aimed to study the time needed for a complete TLS handshake for several network parameters. To this end, based on the approach in ^[10], we created a pair of virtual Ethernets for client–server. In the client's network, a variation of the performance timing program $$ {\tt s\_timer} $$ of the OpenSSL was used to measure the performance as follows: (i) a prescribed number of TLS handshakes was executed, where the relevant post-quantum cipher was embedded each time; and (ii) the session was terminated, storing the time duration that was needed. On the server's side, an Nginx server was executed, which utilized the Open Quantum Safe project's OpenSSL.

We subsequently set several RTTs, depending on the distance assumed between the client and server. Our hypotheses on the RTTs were based on those in ^[10]; as stated therein, four RTTs suffice to illustrate several realistic scenarios, from the optimum one (i.e., the smallest distance) to the worst one (i.e., with the largest distance). These four values of RTTs were $$ 5.368 $$ (best), $$ 30.916 $$ (moderate), $$ 78.448 $$ (bad), and $$ 195.46 $$ ms (worst).

Additionally, we set several values for the packet loss ratio, from $$ 0 $$% to $$ 15 $$%, which seemed to be realistic assumptions according to the information that can be obtained from work in ^[25]. For each cipher, eight different timers (through the $$ {\tt s\_timer} $$ utility) were used, each of them initiating $$ 500 $$ handshakes with the Nginx server — i.e., a total of $$ 4000 $$ connections for each scenario. The device used as a server was the Google cloud. Our experiments were based on the code available in ^[26], which is also a companion to the work presented in ^[10]. The whole setup of this experiment is illustrated in Figure 1.

Figure 1. The setup of the first experiment.

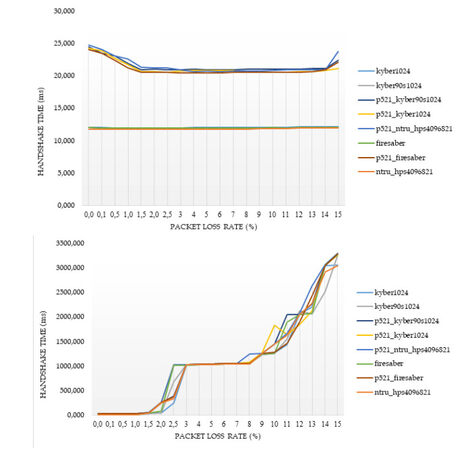
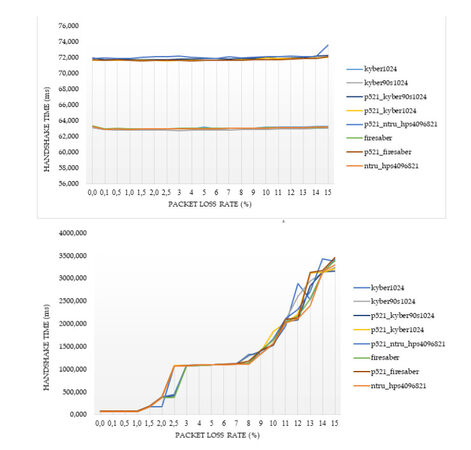
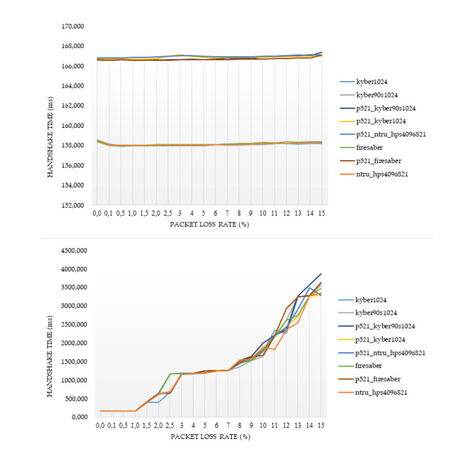
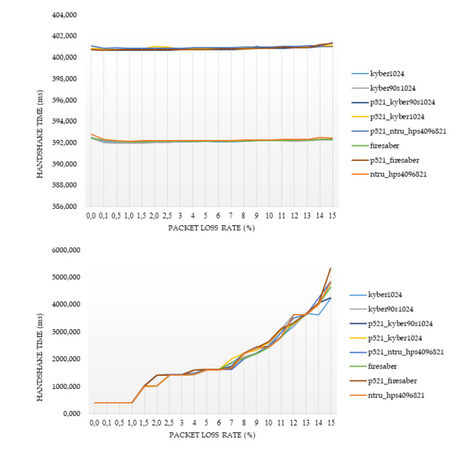
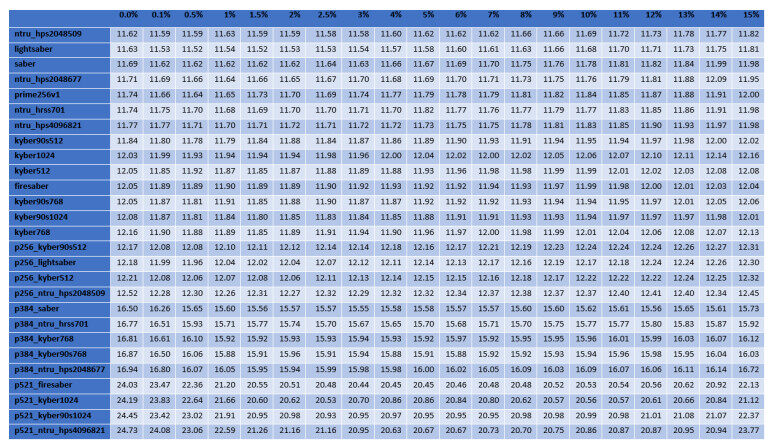
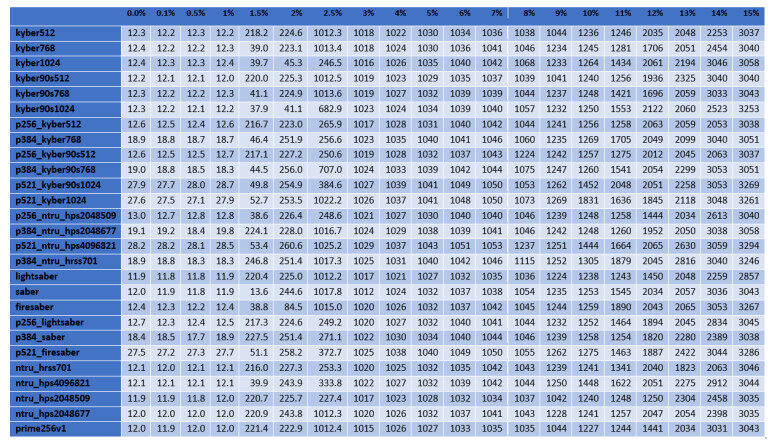
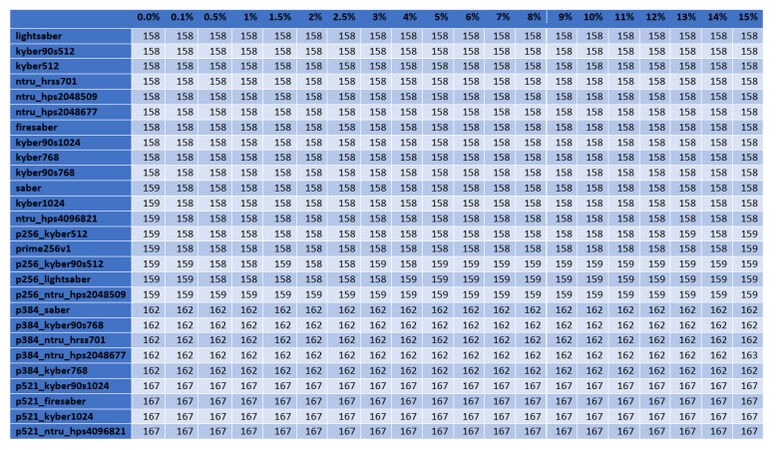
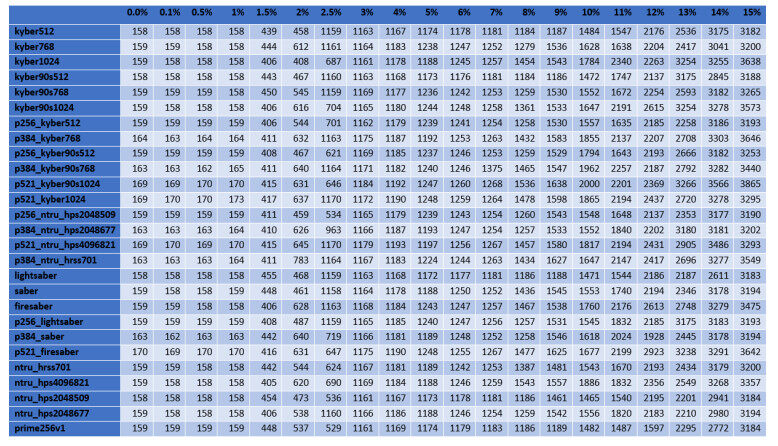
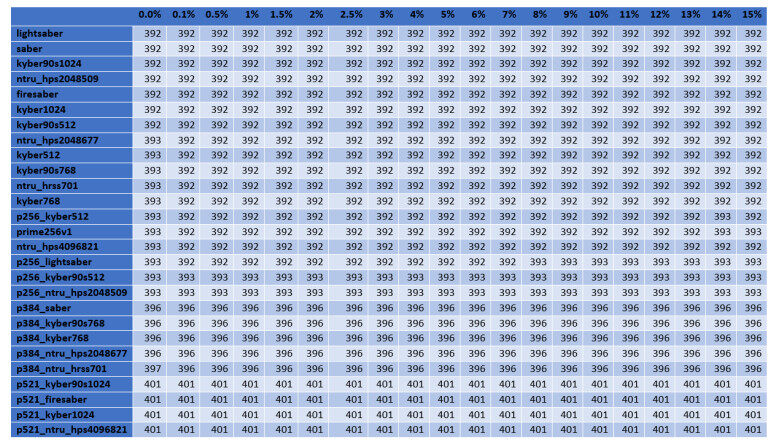
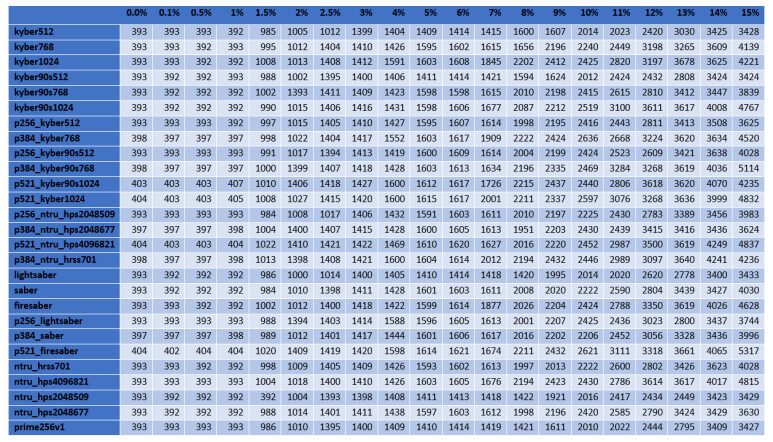
For the cases of ciphers at the highest security level according to the NIST's classification, Figures 2–5 illustrate the diagrams for the time needed to complete the TLS handshakes, for all possible RTTs that were examined (from the best to the worst) and for each possible post-quantum key exchange algorithm. All results from all the experiments, for all security levels, are analytically presented in Figures 13–20 in the Appendix. From these results, we can get the following outcomes:

Figure 2. Results of the time to complete the TLS handshake, for post-quantum ciphers at the highest security level L$$ 5 $$, in conjunction with hybrid implementations as well as with a conventional implementation with elliptic curve Diffie--Hellman key exchange with curve P-$$ 256 $$. The first figure indicates the medians and the second the $$ 95 $$th percentile, for the optimal RTT.

Figure 3. Results of the time to complete the TLS handshake, for post-quantum ciphers at the highest security level L$$ 5 $$, in conjunction with hybrid implementations as well as with a conventional implementation with elliptic curve Diffie--Hellman key exchange with curve P-$$ 256 $$. The first figure indicates the medians and the second the $$ 95 $$th percentile, for the moderate RTT.

Figure 4. Results of the time to complete the TLS handshake, for post-quantum ciphers at the highest security level L$$ 5 $$, in conjunction with hybrid implementations as well as with a conventional implementation with elliptic curve Diffie--Hellman key exchange with curve P-$$ 256 $$. The first figure indicates the medians and the second the $$ 95 $$th percentile, for the bad RTT.

Figure 5. Results of the time to complete the TLS handshake, for post-quantum ciphers at the highest security level L$$ 5 $$, in conjunction with hybrid implementations as well as with a conventional implementation with elliptic curve Diffie--Hellman key exchange with curve P-$$ 256 $$. The first figure indicates the medians and the second the $$ 95 $$th percentile, for the worst RTT.

● The NTRU, Saber, and Kyber variants at the security level L1 behave better than the classical elliptic curve key exchange and their hybrid versions. Even for the few cases that they do not behave better, they are still very close to them, since the worst case that was monitored is a slow down by $$ 2.5\% $$.

● For all security levels, the aforementioned variants seem to behave generally better than their hybrid versions, regardless of the RTT or packet loss ratio.

● A packet loss ratio at $$ 2\% $$ or beyond this value highly affects the overall handshake completion time, regardless of the underlying cipher; such a delay is expected, due to packet re-transmissions resulting from packet losses. As becomes clear from the subsequent experiments, the overall time for the handshake completion is much higher than the time of a pure cryptographic execution, and thus, this experiment is more relevant for assessing the effect of the network rather than the effect of the cipher; the latter was studied in the second experiment.

● The increase of packet loss ratio affects the ciphers at higher security levels L3 and L5 more than the ciphers at the L1 security level.

● For large values of RTT, which correspond to large distances between the client and server, we get that this large distance predominates with respect to the overall performance of completion of the handshake.

In principle, lightsaber seems to achieve the best performance for all network settings, but both Kyber and NTRU are also very close. This comparison was further examined by the subsequent experiments, which focused explicitly on the cryptographic procedure without considering network parameters.

5.2. Second experiment: Comparative study for two different devices under an optimum network

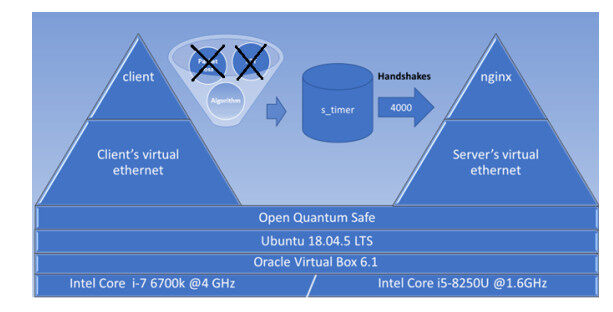
For our second experiment, we fixed the values of RTT and packet loss ratio to zero — i.e., to assume an ideal case with no network delays at all (an optimal network). Our aim was to evaluate the performance of the post-quantum ciphers for different devices with different computing capabilities — i.e., one high_core at $$ 4 $$ GHz (the Google machine) and one low_core at $$ 1.6 $$ GHz (the local machine). The same code as in the first experiment was used, but for each TLS implementation with different post-quantum cipher, we set one timer through the $$ {\tt s\_timer} $$ utility, which initiates $$ 4000 $$ handshakes with the Nginx server. The two local devices were used for the client execution to perform the comparative study. We also examined conventional elliptic curve algorithms to have a comparative study with such contemporary algorithms.

The setup of this experiment is shown in Figure 6.

Figure 6. The setup of the second experiment.

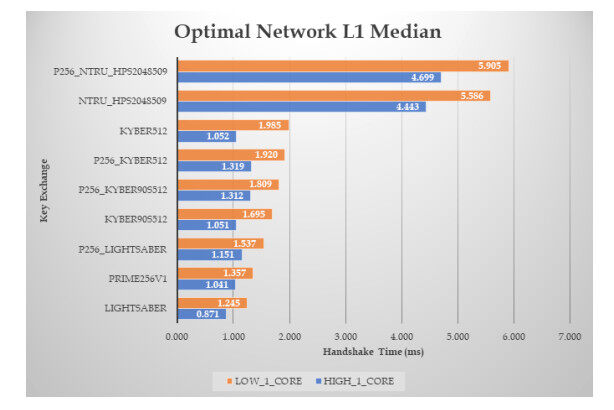
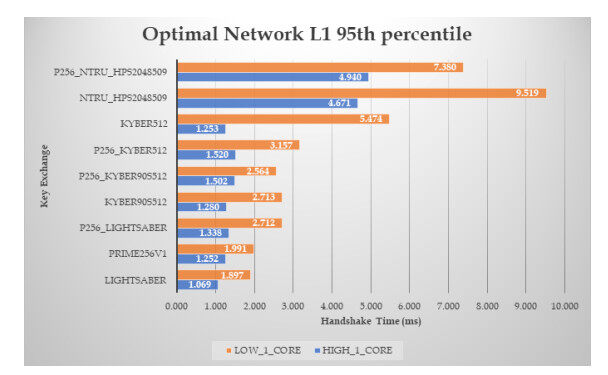
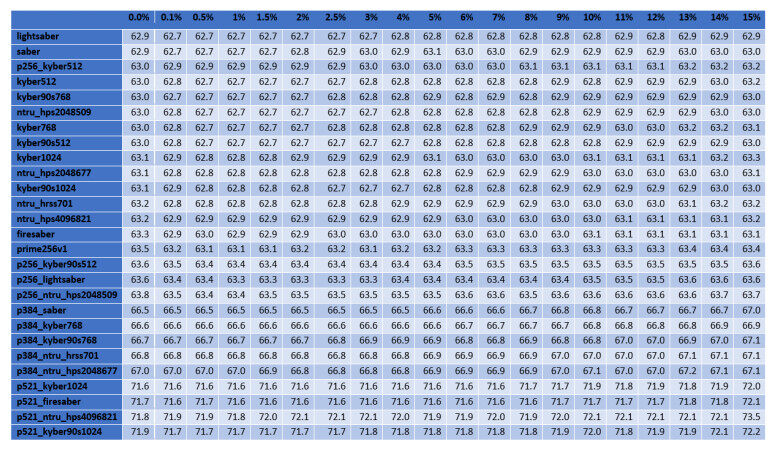
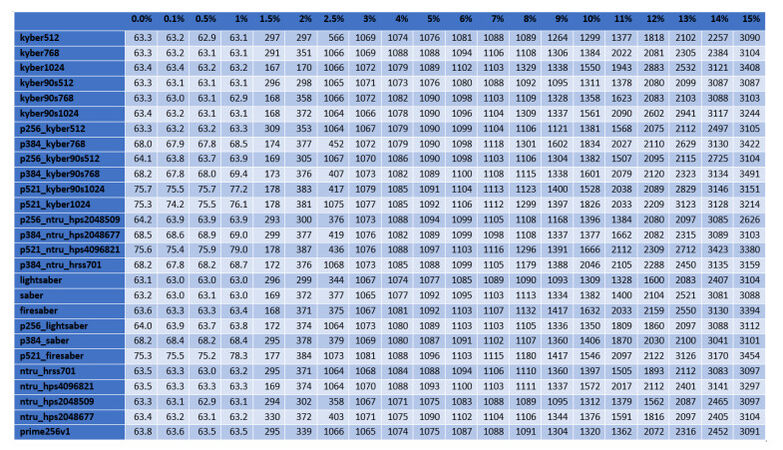
The results are presented in a similar manner as in the first experiments — namely, we computed the medians for the handshake completion time as well the $$ 95 $$th percentile. These measurements took place for all key exchange ciphers with security levels L1, L3, or L5. The results are shown in Figures 7 and 8 for L1 ciphers, Figures 9 and 10 for L3 ciphers, and Figures 11 and 12 for L5 ciphers.

Figure 7. Results of the handshake time, with zero RTT and packet loss ratio, for ciphers at L1 security level (the median time in ms).

Figure 8. Results of the handshake time, with zero RTT and packet loss ratio, for ciphers at L1 security level (the $$ 95 $$th percentile — time in ms).

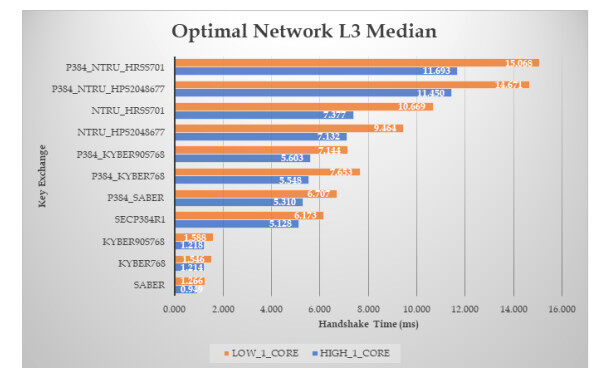
Figure 9. Results of the handshake time, with zero RTT and packet loss ratio, for ciphers at L3 security level (the median time in ms).

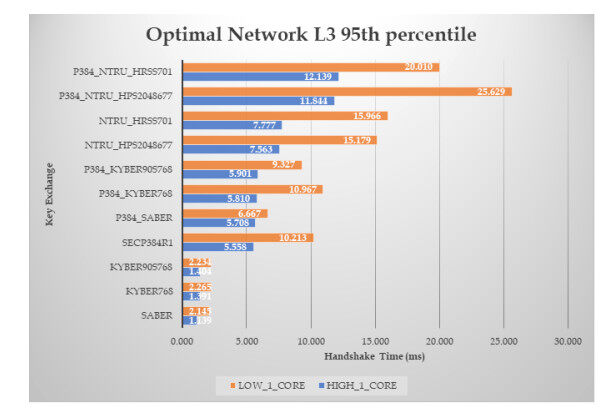
Figure 10. Results of the handshake time, with zero RTT and packet loss ratio, for ciphers at L3 security level (the $$ 95 $$th percentile — time in ms).

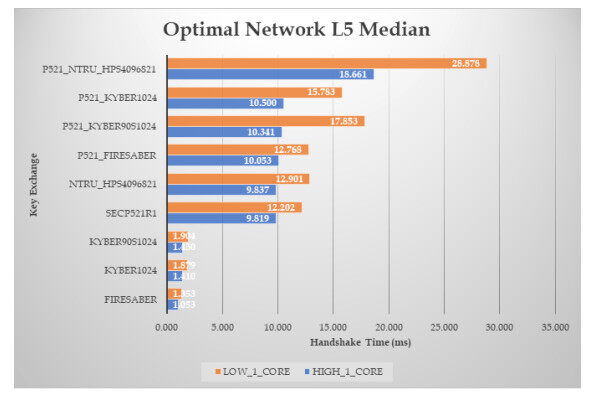
Figure 11. Results of the handshake time, with zero RTT and packet loss ratio, for ciphers at L5 security level (the median time in ms).

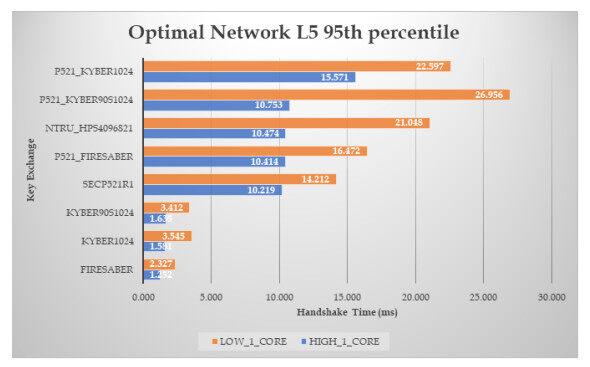
Figure 12. Results of the handshake time, with zero RTT and packet loss ratio, for ciphers at L5 security level (the $$ 95 $$th percentile — time in ms).

Focusing on the L$$ 1 $$ ciphers, we get that the lightsaber seems to be the faster cipher for the key exchange, whereas — as was also apparent in the first experiment, when several network parameters were varied — it seems to be faster even from conventional elliptic curve algorithms with no post-quantum resistance. Moreover, kyber90s512 seems also to have a nice performance. On the contrary, NTRU, as well as its hybrid implementation, seems to have the worst performance, being about $$ 5 $$ times slower than lightsaber and $$ 3.5 $$ times slower than Kyber90s$$ 512 $$; in general, the differences in performance become greater in the high core machine.

Examining, for each post-quantum cipher, how the underlying computing power affects its performance, we get that, moving from the high core to the low core machine, NTRU becomes slower by about $$ 25\% $$, Saber becomes slower by about $$ 42\% $$, and Kyber becomes slower by about $$ 62\% $$, while this decrease in performance for the conventional elliptic curve is about $$ 30\% $$.

Similar conclusions also hold for the L$$ 3 $$ ciphers; in this case, however, the hybrid versions of lightsaber and kyber90s512 seem to be much more slower than in the case of the L1 ciphers. NTRU is $$ 7.5 $$ times slower than Saber and $$ 6 $$ times slower than Kyber$$ 768 $$ (for the high core machine). Moreover, examining how the underlying computing power affects the performance, we get that, moving from the high core to the low core machine, NTRU becomes slower by about $$ 45\% $$, Saber becomes slower by about $$ 33\% $$, and Kyber becomes slower by about $$ 27\% $$, while this decrease in performance for the conventional elliptic curve is about $$ 20\% $$.

The L5 ciphers also have similar behavior and the above conclusions are much more clear; here, Firesaber is about $$ 95\% $$ faster than the elliptic curve algorithm cipher with key length $$ 256 $$ bits. Good performance is also achieved by kyber1024 and kyber90s1024, which is also better than the performance of the conventional elliptic curve algorithm as well as their hybrid versions. Checking NTRU with respect to Saber and Kyber, we get that NTRU is about $$ 9.3 $$ times slower than Firesaber and about $$ 7 $$ times slower than Kyber$$ 1024 $$ (at the high core machine). Moreover, examining how the underlying computing power affects the performance, we get that, moving from the high core to the low core machine, NTRU becomes slower by about $$ 31\% $$, Saber becomes slower by about $$ 28\% $$, and Kyber becomes slower by about $$ 33\% $$, while this decrease in performance for the conventional elliptic curve is about $$ 24\% $$.

For all security levels, and regardless of the underlying computing power (from those two that were used in our experiments), we get that the post-quantum algorithms are faster than their corresponding hybrid versions.

6. DISCUSSION

Combining the above results, it becomes evident that — as expected — the sizes of the key and the ciphertext highly affect the overall performance of a cipher and, thus, a higher security level of the cipher yields degradation in performance. This is particularly obvious for the McEliece cipher, which is an observation that was also pointed out by NIST. More precisely, the McEliece cipher seems to be not an option for classical contemporary systems. Moreover, the NTRU variants seem to also have not as good behavior as Saber and Kyber in terms of performance, even though the relevant key and ciphertext sizes are comparable with those of the other post-quantum secure ciphers.

Moreover, the results also verify that the network parameters also affect the overall performance to a high extent — and, actually, it is a more decisive factor for the overall performance than the underlying cryptographic algorithms that are being used.

In any case, we can conclude that there are several promising solutions for post-quantum key exchange algorithms that can be used in network security protocols such as the TLS, even in conventional contemporary systems. Such ciphers have comparable or, in some cases, even better performance than classical elliptic curve public key algorithms; interestingly, it seems that adopting a hybrid solution does not provide much gain in terms of performance compared to a fully post-quantum secure solution.

As a general conclusion, we can state that all the Saber variants — namely lightsaber, saber, and firesaber — as well as some variants of the Kyber — namely, kyber768, kyber90s768, kyber1024, and kyber90s1024 — could possibly be considered in terms of performance for adoption even for today's computing systems, since they exhibited nice performance properties for all sets of experiments that were carried out. It seems that there is also no need, from the performance point of view, to focus on hybrid implementations, since pure post-quantum secure ciphers seem to have better behavior. This general conclusion seems to remain valid regardless of the underlying computing power.

During the review phase of this paper, NIST completed its third round, as stated above. According to the relative status report that NIST issued ^[27], both KYBER and Saber are suitable for use on constrained devices, as each of these can be implemented (at least without protections against side-channel attacks) using less than $$ 4 $$ kB of RAM with less than 20 kB of storage for the code, while the overall performance of NTRU, Saber, and CRYSTALS-Kyber as KEMs would be acceptable for general-use applications, although NTRU is not quite as good as KYBER or Saber as a result of its slower key generation and somewhat larger public keys and ciphertexts. In the same report, NIST points out that while Saber has the lowest total cost due to its smaller public keys and ciphertexts, the cost difference between KYBER and Saber was not large enough to be considered significant. The algorithm that has been chosen by NIST, as described above, is the CRYSTALS-Kyber. As stated in ^[27], deciding between KYBER, NTRU, and Saber was a difficult choice, since most applications would be able to use any of them without significant performance penalties. Since NIST intended to standardize only one of these finalists, as all three were based on lattices, the final choice was CRYSTALS-Kyber, since NIST found that the security assumption upon which CRYSTALS-Kyber is based is marginally more convincing than the security assumptions of NTRU and Saber, whereas with regard to performance, KYBER was near the top (if not the top) in most benchmarks.

The conclusions derived from the present research are fully in line with the final output of the third round of the NIST competition, since indeed the CRYSTALS-Kyber algorithm chosen by NIST illustrated in our work very good performance (either the best or almost the best) for key exchange in the TLS protocol, whereas the performance benefits of Saber — as pointed out by NIST — are also clear. Moreover, the performance achieved by the CRYSTALS-Kyber is comparable with the classical contemporary public key implementations for the TLS protocol, and this comparison is not actually affected by network parameters.

7. CONCLUSIONS AND FUTURE RESEARCH

This study focused on analyzing the performance of public-key post-quantum algorithms in light of their possible use for key exchange in the prominent TLS protocol. Based on known results and existing software that has already been developed for research purposes, we carry out a more extended set of experiments, taking into account the list of third round finalists of the NIST's standardization process. The main outcome is that there exist differences among the various finalists with respect to their performance, and the main conclusion with regard to the fastest algorithms are in line with the final choice of NIST at the end of this round — namely the choice of CRYSTALS-Kyber as a standard. Moreover, starting from now, employing post-quantum secure solutions into contemporary applications and network security protocols seems to be a viable option. However, even for those algorithms that have not been standardized —i.e. they are not being evaluated anymore in the current fourth round of the NIST evaluation — the results are of importance, taking into account that it cannot be excluded that some of these schemes might be standardized outside the NIST, especially those for which NIST pointed out that they have low "cost" and do not raise (to our current knowledge) security issues. In this regard, it is interesting to recall that Chacha20, which is a secure symmetric cipher supported by TLS $$ 1.3 $$ for encrypting communication data, is not officially standardized by NIST.

This is a highly evolving research field; one should carefully monitor the progress in the NIST evaluation procedure and the related research. Indeed, at the beginning of August 2022, it was announced in a research paper (a pre-print version is currently public ^[28]) that SIKE, which is one of the four algorithms that are currently evaluated by NIST in the fourth round of evaluation (being one of the alternated algorithms in the third round), was cracked by using a computer running Intel Xeon CPU in 1 h.

It should be pointed out that our work focuses only on performance in the handshake phase of the TLS, having post-quantum secure algorithms for key exchange. Although known values of the sizes of the produced ciphertexts and keys are also being presented to allow a comparative study of these factors, we do not explicitly study relevant important parameters such as the bandwidth consumed by communication or the memory required. This could also be considered in future work, taking into account the relevant results announced by NIST. Moreover, the post-quantum digital signature algorithms should also be considered in the same context [such studies have already been performed, for some such algorithms, in several works (e.g., ^[10]), as described in Section $$ 3 $$].

Another important aspect that needs to be considered in future research is to determine the behavior of post-quantum secure TLS implementations in restricted environments in terms of computing power and memory; to this end, it is important to focus on cases of IoT applications (e.g., on mobile devices, a Raspberry Pi, etc.) The current research illustrated that the differences in performance gains — among several post-quantum ciphers — seem to increase with the computing power, but such restricted environments have not been examined. Such research efforts have recently been started (see, e.g., ^[11]).

When dealing with an evaluation of ciphers' performance, it is also of importance to identify which underlying processes/computations are more "heavy", so as to focus appropriately on them in future research for algorithms optimization. This aspect was not studied here, and it constitutes an open research field.

Additionally, focusing on embedding post-quantum secure algorithms in other security protocols residing in lower network architecture levels, such as the IPsec, is also an interesting research area (see, e.g., ^[29]). More generally, focusing on post-quantum solutions in several existing protocols and infrastructures, such as the blockchain ecosystem ^[30], becomes an essential issue in ensuring the appropriate safeguards for long-term data protection.

DECLARATIONS

APPENDIX

All the results obtained from the first experiment are given in Figures 13–20.

Figure 13. Results of the handshake time for the best RTT scenario (the median time in ms).

Figure 14. Results of the handshake for the best RTT scenario (the $$ 95 $$th percentile — time in ms).

Figure 15. Results of the handshake time for the moderate RTT scenario (the median time in ms).

Figure 16. Results of the handshake for the moderate RTT scenario (the $$ 95 $$th percentile — time in ms).

Figure 17. Results of the handshake time for the bad RTT scenario (the median time in ms).

Figure 18. Results of the handshake for the bad RTT scenario (the $$ 95 $$th percentile — time in ms).

Figure 19. Results of the handshake time for the worst RTT scenario (the median time in ms).

Figure 20. Results of the handshake for the worst RTT scenario (the $$ 95 $$th percentile — time in ms).