Original Article | Open Access | 30 Mar 2022

Multi-level storage based auditing scheme for 5G and beyond defined edge computing

Views: 655 | Downloads: 607 | Cited:

Chen Wang^*

Tianqi Zhou

J Surveill Secur Saf 2022;3:16-26.

10.20517/jsss.2021.18 | © The Author(s) 2022.

Author Information

Article Notes

Cite This Article

Abstract

Aim: Edge computing has become one of the most essential approaches for processing user-side data in the future, thanks to the portability of storage and computing devices. 5G and beyond defined edge computing has become one of the most urgently required technologies. However, there are still several issues that must be resolved. Edge computing's present storage structure is incapable of adapting to new and flexible application scenarios. Simultaneously, data stored on edge devices are more vulnerable to attacks, and the integrity of the data needs to be protected.

Method: For 5G and beyond defined edge computing, a novel auditing scheme based on multi-level storage is proposed in this paper. To reduce the response time of data queries, we first present a storage system with neighborhood servers. Then, a scheme for third-party-assisted auditing is described. Users can audit their data using self-defined file names.

Results: The scheme is secure and efficient, according to the security analysis and performance simulation. Our scheme cost less computation overhead than the compared related work.

Conclusion: The result shows that the novel proposal is efficient for the application in 5G and beyond defined edge computing.

Keywords

5G and beyond, edge computing, data auditing, multi-level storage

Download PDF 0 30

INTRODUCTION

With the portability of storage devices and computing devices, edge computing has become one of the important methods for processing user-side data in the future. The advancement of communication technology encourages the improvement of outsourced storage services. For people to establish smart cities and develop distant synchronization activities, 5G and beyond defined edge computing has become one of the most urgently required technologies. The growth of the Internet of Things (IoT) is inextricably linked to the rise of edge computing. Edge computing allows computation to take place at the network's edge, representing both downstream and upstream data from cloud services and IoT devices, respectively. The main idea behind edge computing is to allow computation to take place close to the data source ^[1]. Edge computing will play an increasingly important part in the ongoing iteration of future generations of network technology. In a car network, for example, vehicle equipment communicates with roadside nodes. These roadside nodes can become edge nodes, with computing and storage capabilities to enable real-time data exchange with the vehicle. In similar scenarios, edge computing can not only significantly reduce the system's reaction time but also improve the data storage format.

However, edge computing is confronted with a number of security issues since it is a kind of distributed storage. Due to the lack of external monitoring, data stored at edge nodes may be more easily accessed by attackers. Edge storage space is restricted, and therefore only a portion of the urgently needed data may be saved. As a result, user data may be incomplete in these storage. In response to these issues, academics have begun to investigate data integrity verification schemes that are suited for edge computing ^{[2, 3]}.

The motivation of our work: Edge computing must alter in order to adapt to the new environment, as research and development of 5G and next-generation communication technologies have progressed significantly. As a result, 5G and beyond defined edge computing demands a huge amount of attention. Despite the efforts of many researchers to reduce communication overhead and improve data security in edge computing, there are still several challenges that need to be addressed immediately. The current storage structure for edge computing cannot adapt to new and flexible application scenarios. At the same time, the data stored in edge nodes are frequently incomplete, necessitating the collaboration of a new server storage and transmission system as well as a new audit scheme to ensure its integrity.

Our contributions: The main contributions of this paper are listed as follows:

● A multi-level storage system model is proposed for 5G and beyond defined edge computing. In view of the immediacy of 5G and beyond networks, this paper presents a multi-level storage edge computing system to adapt to changing application circumstances. Cloud servers, edge servers, and neighborhood servers are all part of the system. It is worth noting that, in this proposal, any mobile device with storage and processing functions can be used as these small neighborhood servers. The user's frequently used data are saved in the closest severs to them, and the user's data request is handled with a quick response.

● The integrity audit of the sampling of data based on self-defined file names is realized. A file data auditing scheme is presented based on self-defined file names to adapt to decentralized file storage. This scheme allows users to sample and audit their data stored on the server. To accomplish this, the user merely needs to encrypt the file name that needs to be audited and transmit it to the third-party administrator (TPA). TPA completes the integrity verification of user data without revealing any user's personal information.

Organization

The rest of this paper is laid out as follows. Section 2 gives the related work of auditing and edge computing technologies. Section 3 introduces some of the paper's preliminaries, such as bilinear pairing and ID-based signature. Section 4 shows the system model and the security model of this paper. Section 5 presents the main idea of this paper. Section 6 presents the security analysis and performance simulation. Finally, in Section 7, the conclusions are drawn.

RELATED WORK

The power of cloud computing received a lot of attention before edge computing received much publicity. Cloud storage data integrity has also received much interest. Public auditing was proposed by Ateniese et al.^[4]. In 2017, Shen et al. proposed a public cloud data auditing scheme with dynamic structure^[5].

Edge computing was first proposed in 2012 by Bonomi et al.^[6], and it is believed that this technology will be very suitable for the development of the Internet of Things. Mobile edge computing is considered as one of the key emerging technologies for 5G networks ^[7]. The development of 5G and beyond defined edge computing requires rapid developing technologies. The data integrity verification of edge computing is deemed highly crucial to effectively serve data outsourcing consumers using edge computing.

At present, a lot of work has been done in this field to promote the further popularization and use of edge computing technology. Alwarafy et al.^[8] surveyed the security and privacy issues of Internet of Things-based edge computing. They considered auditing as one of the important issues for the development of edge computing. ZSS signature scheme was introduced to provide public auditing for edge computing by Wang et al.^[9]. Tong et al.'s ^[2] new proposal can achieve data integrity verification on a single edge or multiple edges. A security framework for big data analysis based on edge computing was proposed by Garg et al.^[10]. A lightweight sampling-based probabilistic scheme for app developers was proposed by Li et al.^[11] to audit the integrity of data stored on a wide scale of edge servers. The novel proposal of Li et al.^[3] has the capability of inspecting the integrity of data on the edge severs and locating corrupted data.

PRELIMINARIES

Some required preliminaries used in this paper, such as bilinear pairing and ID-based signature, are listed in this section.

Bilinear Pairing

$$ \mathbb{G}_1 $$ and $$ \mathbb{G}_2 $$ are considered as two groups with prime order $$ q $$ , where $$ \mathbb{G}_1 $$ is an additive group and $$ \mathbb{G}_2 $$ is a multiplicative group. A cryptographic bilinear map is a mapping $$ e $$ on $$ \left( \mathbb{G}_1, \mathbb{G}_2 \right) $$ : $$ \mathbb{G}^2_1 \rightarrow \mathbb{G}_2 $$ that satisfies the characteristics listed below ^[12].

Bilinearity.$$ e\left( aP, bQ\right) = e\left( P, Q\right)^{ab} $$ for all $$ P, Q \in \mathbb{G}_1 $$ and $$ a, b \in Z_q^* $$ .The following is a description of how this could be expressed. For $$ P, Q, R \in \mathbb{G}_1 $$ , $$ e(P + Q, R) = e(P, R) e(Q, R) $$ and $$ e(P - Q, R) = e(P, R) e(Q, R)^{-1} $$ .

Non-degeneracy. Let $$ P $$ be a generator of $$ \mathbb{G}_1 $$ . $$ e(P, P) $$ is a generator of $$ \mathbb{G}_2 $$ . To put it another way, $$ e(P, P) \neq 1 $$ .

Computability.$$ e $$ is efficiently computable.

ID-based Signature

The first scheme of ID-based signature from pairings (IDS) was presented by Hess ^[13]. IDS is made up of four algorithms: Setup, Extract, Sign, and Verify.

Setup: The trust authority generates a public key using a random number as a secret key.

Extract: The trust authority runs this algorithm when a signer requests the secret key that corresponds to their identity. The trust authority then provides the signer with the identity's secret key.

Sign: The signer is in charge of this algorithm. The signer encrypts the message using their identity's secret key.

Verify: The receiver verifies the received signed message and outputs the result of whether the signature is valid or not.

SYSTEM AND SECURITY MODELS

System Model

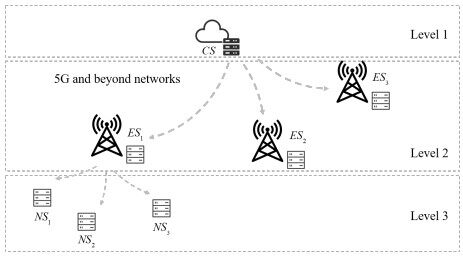
The proposed scheme's system model is introduced in this section. The construction of a multi-level storage system for 5G and beyond defined edge computing is shown in Figure 1. The demand for edge computing has resulted in a wide range of storage options. The multi-level storage presented in this study attempts to reduce the time it takes for users to access data and to ensure that damaged data may be recovered. There are three main levels of servers for data storage and processing, as indicated in Figure 1: cloud server (CS), edge servers (ESs), and neighborhood servers (NSs). A user's complete data are stored in CS. The cloud server can also be distributed in a real-world network system. We utilize a CS to represent the role of a cloud formed by all cloud servers for ease of description. Multiple ESs are subordinated by CS. These ESs keep track of a user's incomplete data in different geographic locations and application contexts. All user data are separated and stored in each ES, ensuring that the CS and ES can complement each other in the event that data in one are damaged. NSs also refer to small servers that are placed near users. These servers often retain data that are frequently accessed by users. To fulfill the actual application requirements of 5G and beyond defined edge computing, this system enables users to acquire data access and processing services faster.

Multi-level storage based auditing scheme for 5G and beyond defined edge computing

Figure 1. The construction of the proposed multi-level storage system.

Security Model

The proposed scheme's security model is provided here. Designing a security model fit for the environment of 5G and beyond defined edge computing, based on the system model given in detail above, is critical to the scheme's design and security evaluation. Servers (including CS, ESs, and NSs), third-party administrators (TPAs), and users are the three most essential roles in this system. The following is a collection of the three roles' detailed security definitions.

● Severs: All servers are considered to be likely to tamper with data or lose some of the data due to poor management. The server provides users with data outsourcing services to ensure the integrity of the data. However, due to external factors, such as natural disasters and human-caused damage, or internal factors, such as malicious cloud server deliberate destruction, user data may be missing. In addition, malicious servers may tamper with user data, thereby causing the destruction of users' personal information.

● Third party administrator (TPA): TPA refers to the administrator who is responsible for helping users generate data tags and verify data integrity in the system. TPA is believed to be able to faithfully perform the data integrity verification operation procedures set by the system. However, TPA may be curious about the content of the data and try to obtain user privacy information by obtaining the original data.

● Users: Users refer to users who use edge computing services in this system. The attacker may reach the user's data by pretending to be a legitimate user. A forged user needs to be identified to ensure the security of user data.

METHODS

In this section, the main idea of this novel scheme is presented.

Overview of the Proposal

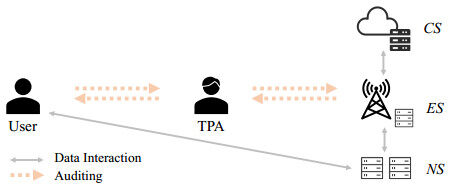
This subsection provides an overview of the proposed multi-level storage-based auditing scheme, which is shown in Figure 2. The user and the servers perform data interaction, and the servers interact at different levels based on the data requested by the user. When a user needs to access data, for example, he or she typically sends a data request instruction to his or her nearest neighborhood server (NS). The NS validates whether the data required by the user has a complete backup on this server after getting the instruction. If a relevant sequence is not kept on this server, it will seek it out from a peer or superior server. The user has the option of requesting an audit of the data gathered. A third-party administrator (TPA) contributes to the data audit. The user provides the TPA with the file name of the data to be audited as well as other required parameters. Based on these file names, TPA generates an audit challenge and sends it to the server. The server generates and returns a data integrity proof according to the challenge to the TPA. The TPA checks the proof and informs the user of the outcome. It is worth mentioning that servers at all levels give proof of data integrity verification as a whole in this scheme.

Figure 2. The overview of the proposed scheme.

The detailed scheme

The proposed scheme is described in detail in this subsection. The proposed scheme's file name upload and auditing processes are depicted in Figure 3. The technique is divided into two parts: the file name upload phase and the auditing phase.

Figure 3. The file name upload and auditing processes of the proposed scheme

File name upload phase

This phase primarily discusses how the user assigns file names to all data file blocks and creates signature tags for each file name. The encrypted file name, together with the accompanying tag, will be provided to the TPA. This data are saved in the TPA. It is worth mentioning that, when a user uploads data files to the server, the same encrypted file names are attached to them.

First, with prime order $$ q $$ , an additive group $$ \mathbb{G}_1 $$ and a multiplicative group $$ \mathbb{G}_2 $$ are chosen. On $$ \left( \mathbb{G}_1, \mathbb{G}_2 \right), $$ there is a bilinear map $$ e $$ : $$ \mathbb{G}^2_1 \rightarrow \mathbb{G}_2 $$ . As the master key, a random number $$ \alpha \in Z_{q^{\rm{*}}} $$ is chosen, and $$ P_{pub} $$ is set to $$ P_{pub} = \alpha P $$ . The following five hash functions are used: $$ H_0 $$ , $$ H_2 $$ : $$ \{0, 1\} \to \mathbb{G}_1 $$ , $$ H_1 $$ : $$ \mathbb{G}_1 \to \mathbb{G}_1 $$ , and $$ H_3 $$ : $$ \mathbb{G}_2 \to \{0, 1\}^{len} $$ . $$ (\mathbb{G}_1, \mathbb{G}_2, e, P, P_{pub}, H_1, H_2, H_3, H_4, len ) $$ are the system parameters. A user with identity $$ UID $$ calculates its private key $$ S=\alpha H_2(UID) $$ .

The user wishes to upload a number of files, which are denoted as data in a set $$ \{m_i\}_{i \in N} $$ with $$ N $$ blocks of data in the set. Random values $$ x $$ , $$ y $$ are chosen from $$ {\mathbb{Z}_p} $$ , and $$ X = xP $$ and $$ Y = yP $$ are calculated for each file $$ m_i $$ . The user sets a file name $$ f_i $$ for each block of data $$ m_i $$ . The file name is encrypted as $$ {F_i} = y{H_0}\left( {{f_i}} \right) $$ . Then, the corresponding tag $$ {\sigma _i} $$ of the file name is calculated as follows.

$$ {\sigma _i} = \frac{{{m_i}}}{x}\left( {{H_1}\left( {{F_i}} \right) + S} \right), $$

where $$ S $$ is the private key calculated by the user's $$ UID $$ .

Parameters that need to be sent to the TPA are listed in a message $$ fname = \left( {X, \left\{ {{\sigma _i}} \right\}, \left\{ {{F_i}} \right\}, Y, {\mathop{\rm IDS}\nolimits} \left( {X||\sum\nolimits_{i \in N} {{F_i}} } \right)} \right) $$ . The message $$ fname $$ is sent to TPA and TPA verify the signature $$ IDS\left( {X||\sum\nolimits_{i \in N} {{F_i}} } \right) $$ . Then, the important message will be stored in the memory of the TPA.

Data integrity auditing phase

When the user wants to audit the integrity of some of the upload data, he or she needs to pick out the files and the encrypted files' names are denoted as $$ \left\{ {{F_j}} \right\}{\kern 1pt} {{\kern 1pt} _{j \in Q}}{\kern 1pt} {\kern 1pt} {\kern 1pt} $$ (let us consider the number of the selected files as $$ Q $$ ). This set of encrypted file names for data auditing is sent to the TPA. The TPA chooses different random values $$ \upsilon _j $$ . The pairs are denoted as $$ \left\{ {{\rho _j}} \right\}{\kern 1pt} {\kern 1pt} {{\kern 1pt} _{j \in Q}} \leftarrow \left\{ {\left( {{F_j}, {\upsilon _j}} \right)} \right\}{\kern 1pt} {{\kern 1pt} _{j \in Q}} $$ . A random value $$ \beta $$ is chosen by TPA from $$ {\mathbb{Z}_p} $$ , and $$ \varphi = \beta P $$ is calculated with $$ \beta $$ . Then, the following value is calculated for each $$ \upsilon _j $$ :

$$ {K_j} = e{\left( {{\upsilon _j}{H_2}\left( {UID} \right), {P_{pub}}} \right)^\beta }, $$

where $$ UID $$ is the identity of the user who requests the auditing and $$ P_{pub} $$ is the one of the public parameter of the user. All these $$ K_j $$ are multiplied together as $$ K = \prod\nolimits_{j \in Q} {{K_j}} $$ . Then, $$ chal = \left( {\varphi , K, \left\{ {{\rho _j}} \right\}} \right) $$ is sent as a challenge to the server.

The server looks for the relevant original data file after receiving the challenge. The server will request data from other servers if the desired data are not accessible locally. The three values $$ V $$ , $$ M $$ , and $$ L $$ are calculated as: $$ V = \sum\nolimits_{j \in Q} {{\upsilon _j}} $$ , $$ M = \sum\nolimits_{j \in Q} {{m_j}} $$ , and $$ L = \sum\nolimits_{j \in Q} {{m_j}{H_1}\left( {{F_j}} \right)} $$ , respectively. The proof of the integrity auditing is computed as follows:

$$ proof = {H_3}\left( {e{{\left( {L, \varphi } \right)}^V}{K^M}} \right). $$

The $$ proof $$ is sent to TPA. TPA verifies the $$ proof $$ by the following equation.

$$ proof \stackrel{?}{=} {H_3}\left( {\prod\nolimits_{j \in Q} {e\left( {{\upsilon _j}{\sigma _j}, \beta X} \right)} } \right). $$

If the equation holds, the integrity of the data is considered to be proven. Otherwise, the system needs to check out whether the data on the servers has been changed.

RESULTS

The performance of the proposed scheme is provided in this section, including the security analysis and performance simulation.

Security analysis

In this section, we first analysis the correctness of the proposal. Then, according to our security model, the security of the scheme can be analyzed in three aspects: security against a malicious sever, security against an honest but curious TPA, and security against a forged user.

Correctness

The correctness of the scheme can be shown by the following equation.

$$ \begin{array}{l} {H_3}\left( {e{{\left( {L, \varphi } \right)}^V}{K^M}} \right)\\ = {H_3}\left( {e{{\left( {\sum\nolimits_{j \in Q} {{m_j}{H_1}\left( {{F_j}} \right)} , \varphi } \right)}^{\sum\nolimits_{j \in Q} {{\upsilon _j}} }}{{\prod\nolimits_{j \in Q} {{K_j}} }^{\sum\nolimits_{j \in Q} {{m_j}} }}} \right)\\ = {H_3}\left( {e{{\left( {\sum\nolimits_{j \in Q} {{m_j}{H_1}\left( {{F_j}} \right)} , \beta P} \right)}^{\sum\nolimits_{j \in Q} {{\upsilon _j}} }}{{\prod\nolimits_{j \in Q} {e\left( {{\upsilon _j}{H_2}\left( {UID} \right), \alpha P} \right)} }^{\beta \sum\nolimits_{j \in Q} {{m_j}} }}} \right)\\ = {H_3}\left( {\prod\nolimits_{j \in Q} {e\left( {{\upsilon _j}{m_j}{H_1}\left( {{F_j}} \right), \beta P} \right)} \prod\nolimits_{j \in Q} {e\left( {{\upsilon _j}{m_j}\alpha {H_2}\left( {UID} \right), \beta P} \right)} } \right)\\ = {H_3}\left( {\prod\nolimits_{j \in Q} {e\left( {{\upsilon _j}\frac{{{m_j}}}{x}\left( {{H_1}\left( {{F_j}} \right) + \alpha {H_2}(UID)} \right), \beta xP} \right)} } \right)\\ = {H_3}\left( {\prod\nolimits_{j \in Q} {e\left( {{\upsilon _j}\frac{{{m_j}}}{x}\left( {{H_1}\left( {{F_j}} \right) + S} \right), \beta X} \right)} } \right)\\ = {H_3}\left( {\prod\nolimits_{j \in Q} {e\left( {{\upsilon _j}{\sigma _j}, \beta X} \right)} } \right) \end{array} $$

Obviously, the proof can be accepted if the equation stands.

Security against a malicious sever

A malicious server may attempt to modify or delete user data on the server. In this scheme, if the sever cannot provide complete data block $$ m_i $$ , the values $$ M = \sum\nolimits_{j \in Q} {{m_j}} $$ and $$ L = \sum\nolimits_{j \in Q} {{m_j}{H_1}\left( {{F_j}} \right)} $$ cannot be correctly calculated. Without correct $$ M $$ and $$ L $$ , the server cannot provide a correct proof to the TPA. Obviously, once a user requests an audit on the data, the server cannot provide the correct audit result even if the data have been tampered with.

Security against an honest but curious TPA

An honest but curious TPA can perform the operations prescribed by the system and complete the auditing process, but such a TPA may be interested in the audited data content or user-defined file names. In this paper, the TPA only receives some encrypted file names $$ {F_i} = y{H_0}\left( {{f_i}} \right) $$ . Thus, the TPA cannot know the names defined by the user. Besides, the TPA uses the tag $$ {\sigma _i} $$ of the data $$ m_i $$ and verifies the $$ proof $$ from the sever without knowing the context of $$ m_i $$ .

Security against a forged user

An attacker may want to obtain data by forging a legitimate user. However, in this scheme, a forged user cannot obtain any data except the result that the user's data are complete. Obtaining data requires IDS authentication. The attacker does not have the user's private key, so they cannot perform the corresponding authentication.

Simulation

Suppose that $$ i $$ is the number of uploaded files and $$ j $$ is the number of selected files. The user needs to perform 2+2$$ i $$ multiplication operations and 2$$ i $$ hash to point function operations. The TPA needs to perform $$ j $$ +1 multiplication operations, one hash to point function, $$ j $$ pairing operations, and $$ j $$ exponentiation operations for challenge generation. The TPA also needs to perform $$ j $$ +1 multiplication operations and $$ j $$ pairing operations for proof verification. The server needs to perform $$ j $$ multiplication operations, $$ j $$ hash to point function, one pairing operation, and two exponentiation operations for a proof generation.

The simulation of the proposed auditing scheme was implemented with the GNU Multiple Precision Arithmetic (GMP) library and Pairing-Based Cryptography (PBC) library, using C language on a Raspberry Pi B with Ubuntu 18.04 TLS, 3.2GHz Intel(R) Core(TM) i5-6400, 8G of RAM.

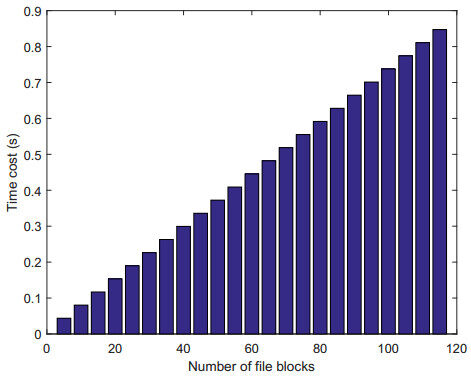
Figures 4 and 5 show the result of the simulation. In Figure 4, the user will spend more time and overhead on the generation of file name tags as the number of data blocks increases, that is, as the value of $$ N $$ grows larger. These operations, however, can be conducted offline; therefore, the audit process is unaffected. In Figure 5, the computation cost of TPA and server will steadily increase as the number of files that need to be audited grows, i.e., as the Q value grows. The server must obviously take longer to generate a proof. However, since the TPA and server's computational power is unrestricted, the cost of the two terminals can be ignored and the time for verification is acceptable. In conclusion, the scheme proposed in this paper is efficient.

Figure 4. The time cost for user to generate tags.

Figure 5. The computation cost for TPA and the sever to perform data auditing.

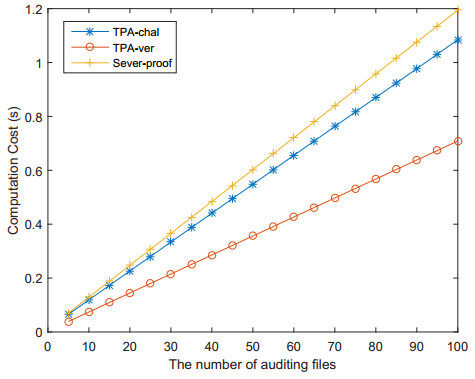
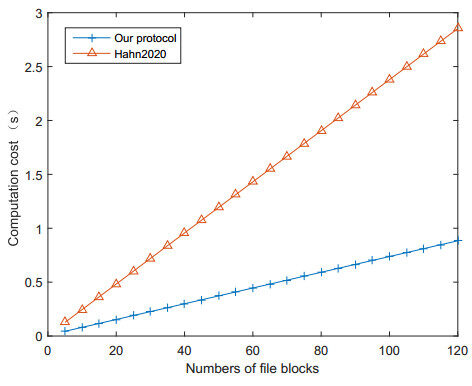
To show the efficiency of our proposed protocol, simulations of our protocol and the related work by Hahn ^[14] were implemented. As shown in Figure 6, the users in our protocol require less computation cost.

Figure 6. The computation cost compared with related work.

DISCUSSION

In this paper, a novel auditing scheme based on multi-level storage is proposed for 5G and beyond defined edge computing. We first propose a storage system with neighborhood servers to improve the response speed of data requests. Then, a third-party-assisted auditing scheme is presented. The novel scheme allows users to audit their data according to self-defined file names. The security analysis and performance simulation show that the scheme is secure and efficient.

DECLARATIONS

Authors' contributions

Made substantial contributions to conception and design of the study and performed data analysis and interpretation: Wang C, Zhou T

Performed data acquisition, as well as provided administrative, technical, and material support: Wang C

Availability of data and materials

Not applicable.

Financial support and sponsorship

This work is supported by the National Natural Science Foundation of China under Grants No. 61922045, No. 61877034, No. U1836115, No. 61672290, the Natural Science Foundation of Jiangsu Province under Grant No. BK20181408, the State Scholarship Fund by the China Scholarship Council under No. 202008320536, and No. 202109040028.

Conflicts of interest

All authors declared that there are no conflicts of interest.

Ethical approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Copyright

REFERENCES

1. Shi W, Cao J, Zhang Q, Li Y, Xu L. Edge computing: Vision and challenges. IEEE internet of things journal 2016;3:637-46.

2. Tong W, Jiang B, Xu F, Li Q, Zhong S. Privacy-Preserving Data Integrity Verification in Mobile Edge Computing. In: 2019 IEEE 39th International Conference on Distributed Computing Systems (ICDCS); 2019. pp. 1007-18.10.1109/ICDCS. 2019.00104.

3. Li B, He Q, Chen F, Jin H, Xiang Y, et al. Inspecting Edge Data Integrity with Aggregated Signature in Distributed Edge Computing Environment. IEEE Transactions on Cloud Computing 2021; doi: 10.1109/TCC.2021.3059448.

4. Ateniese G, Burns R, Curtmola R, Herring J, Kissner L, et al. Provable data possession at untrusted stores. In: Proceedings of the 14th ACM conference on Computer and communications security; 2007. pp. 598-609.10.1145/1315245.1315318.

5. Shen J, Shen J, Chen X, Huang X, Susilo W. An Efficient Public Auditing Protocol With Novel Dynamic Structure for Cloud Data. IEEE Transactions on Information Forensics and Security 2017;12:2402-15.

6. Bonomi F, Milito R, Zhu J, Addepalli S. Fog computing and its role in the internet of things. In: Proceedings of the first edition of the MCC workshop on Mobile cloud computing; 2012. pp. 13-16.10.1145/2342509.2342513.

7. Hu YC, Patel M, Sabella D, Sprecher N, Young V. Mobile edge computing—A key technology towards 5G. ETSI white paper 2015;11:1-16.

8. Alwarafy A, Al-Thelaya KA, Abdallah M, Schneider J, Hamdi M. A Survey on Security and Privacy Issues in Edge-Computing-Assisted Internet of Things. IEEE Internet of Things Journal 2020;8:4004-22.

9. Wang H, Zhang J, Lin Y, Huang H. ZSS Signature Based Data Integrity Verification for Mobile Edge Computing. In: 2021 IEEE/ACM 21st International Symposium on Cluster, Cloud and Internet Computing (CCGrid); 2021. pp. 356-65.10.1109/CCGrid51090.2021.00045.

10. Garg S, Singh A, Kaur K, Aujla GS, Batra S, et al. Edge Computing-Based Security Framework for Big Data Analytics in VANETs. IEEE Network 2019;33:72-81.

11. Li B, He Q, Chen F, Jin H, Xiang Y, et al. Auditing cache data integrity in the edge computing environment. IEEE Transactions on Parallel and Distributed Systems 2020;32:1210-23.

12. Boneh D, Franklin MK. Identity-Based Encryption from the Weil Pairing. In: Kilian J, editor. Advances in Cryptology - CRYPTO 2001, 21st Annual International Cryptology Conference, Santa Barbara, California, USA, August 19-23, 2001, Proceedings. vol. 2139 of Lecture Notes in Computer Science. Springer; 2001. pp. 213-29.10.1007/3-540-44647-8_13.

13. Hess F. Efficient Identity Based Signature Schemes Based on Pairings. In: Nyberg K, Heys HM, editors. Selected Areas in Cryptography, 9th Annual International Workshop, SAC 2002, St. John's, Newfoundland, Canada, August 15-16, 2002. Revised Papers. vol. 2595 of Lecture Notes in Computer Science. Springer; 2002. pp. 310-24.10.1007/3-540-36492-7_20.

14. Hahn C, Kwon H, Kim D, Hur J. Enabling fast public auditing and data dynamics in cloud services. IEEE Transactions on Services Computing 2020; doi: 10.1109/TSC.2020.3030947.

Cite This Article

Export citation file: BibTeX | RIS

OAE Style

Wang C, Zhou T. Multi-level storage based auditing scheme for 5G and beyond defined edge computing. J Surveill Secur Saf 2022;3:16-26. http://dx.doi.org/10.20517/jsss.2021.18

AMA Style

Wang C, Zhou T. Multi-level storage based auditing scheme for 5G and beyond defined edge computing. Journal of Surveillance, Security and Safety. 2022; 3(1): 16-26. http://dx.doi.org/10.20517/jsss.2021.18

Chicago/Turabian Style

Wang, Chen, Tianqi Zhou. 2022. "Multi-level storage based auditing scheme for 5G and beyond defined edge computing" Journal of Surveillance, Security and Safety. 3, no.1: 16-26. http://dx.doi.org/10.20517/jsss.2021.18

ACS Style

Wang, C.; Zhou T. Multi-level storage based auditing scheme for 5G and beyond defined edge computing. J. Surveill. Secur. Saf. 2022, 3, 16-26. http://dx.doi.org/10.20517/jsss.2021.18

About This Article

Copyright

© The Author(s) 2022. Open Access This article is licensed under a Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, sharing, adaptation, distribution and reproduction in any medium or format, for any purpose, even commercially, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Data & Comments

Data

Views

655

Downloads

607

Citations

Comments

Comments

Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.

⁰

Download PDF

Download XML 2 downloads

Cite This Article 14 clicks

Export Citation 32 clicks

Like This Article 30 likes

Share This Article

https://www.oaepublish.com/articles/jsss.2021.18

Scan the QR code for reading!

See Updates

Contents

Figures

Multi-level storage based auditing scheme for 5G and beyond defined edge computing

Abstract

Keywords

INTRODUCTION

Organization

RELATED WORK

PRELIMINARIES

Bilinear Pairing

ID-based Signature

SYSTEM AND SECURITY MODELS

System Model

Security Model

METHODS

Overview of the Proposal

The detailed scheme

File name upload phase

Data integrity auditing phase

RESULTS

Security analysis

Correctness

Security against a malicious sever

Security against an honest but curious TPA

Security against a forged user

Simulation

DISCUSSION

DECLARATIONS

Authors' contributions

Availability of data and materials

Financial support and sponsorship

Conflicts of interest

Ethical approval and consent to participate

Consent for publication

Copyright

REFERENCES

Cite This Article

About This Article

Copyright

Data & Comments

Data

Comments

Share This Article

See Updates

Committee on Publication Ethics

Portico

Committee on Publication Ethics

Portico