Leakless privacy-preserving multi-keyword ranked search over encrypted cloud data
Abstract
Aim: During the last decade, various type of cloud services have encouraged individuals and enterprises to store personal data in the cloud. Despite its flexibility, cost efficiency, and convenient service, protecting security and privacy of the outsourced data has always been a primary challenge. Although data encryption retains the outsourced data’s security and privacy to some extent, it does not permit traditional plaintext keyword search mechanisms, and it comes at the cost of efficiency. Hence, proposing an efficient encrypted cloud data search service would be an important step forward. Related work focuses on single keyword search and even those which support multi-keyword search suffer from private information leakage.
Methods: Our proposed method, employs the secure inner product similarity and our chaining encryption notion. The former helps to provide sufficient search accuracy and the latter yields the privacy requirements.
Results: In this paper, we address the problem of leakless privacy-preserving multi-keyword ranked search over encrypted cloud data (LRSE), and our new contributions address challenging problems of search pattern, and cooccurrence information leakage in the cloud.
Conclusion: Our security and performance analysis shows that the proposed scheme guarantees a high level of privacy/security and efficiency.
Keywords
1 Introduction
With the advent of cloud computing, data owners are motivated to outsource their personal data from local repositories to the cloud to increase flexibility, convenience and to reduce the burden of the local data maintenance costs. However, the privacy of the data must be preserved against unwanted, unauthorized, and malicious accesses from outside attackers and unapproved insiders, including systems such as cloud servers. To access the data, unlike external attackers that must develop smart and subtle ways to circumvent security firewalls and access-control mechanisms, the cloud accesses data directly, which is the reason it is considered a primary privacy threat.
Encrypting the data before it is transferred to the cloud protects the data to some extent, but at the cost of efficiency. Posing queries on the encrypted data so it is searchable is one the current open challenges. Even though Searchable Symmetric Encryption (SSE) enables search on ciphertext, these schemes support only Boolean keyword search, i.e., whether a keyword exists in a document or not[1-7]. Moreover, these schemes must strike a balance between security and efficiency[8]. Consequently, the documents retrieved may be incorrect or incomplete which consumes more time, computation power, and network bandwidth. Conversely, disclosing more information to the cloud to increase accuracy and query efficiency, leads to further privacy exposure.
Multi-keyword ranked search over encrypted cloud data (MRSE) schemes have been proposed[9-11] to (1) acquire result relevance ranking, instead of returning undifferentiated results; and (2) improve search result accuracy by supporting multiple keywords search instead of single keyword search which often yields in unacceptably coarse results. Consequently, each keyword refines the results further. Moreover, the cloud is able to rank the results based on their relevance and returns the top-k most relevant data items which causes less network bandwidth consumption, increased data user’s satisfaction, and is highly desirable in the “pay-as-you-use” cloud paradigm[9].
Although MRSE schemes [9-11] are helpful and allow a user to search and retrieve the documents of interest, they suffer from private information leakage. Query algorithms for existing MRSE schemes are mostly deterministic, which means the same keyword can be used for the same type of queries. Thus, the attacker is able to determine whether the keywords retrieved by two queries are the same[12] (search pattern attack). Moreover, some words often co-occur with other words so the attacker can determine keywords with similar term of distribution (co-occurrence attack)[11]. For instance, the bigram “of the” occurs much more frequently than any other bigrams in English language[13]; and possessing some auxiliary knowledge can disclose more information about the co-occurring terms. For example, the term “united” is very likely to co-occur with “states” in White House official paperwork. Thus, identifying a term is not difficult when the attacker knows the corresponding co-occurring term in the ciphertext. Further, documents in the same category share a considerable overlap of terms and keywords so information leakage in one document can lead to privacy violation in other documents. In addition, during each search, tracking the keywords and the corresponding retrieved documents can leak more information (access pattern attack). Thus, to preserve the data privacy, this information must be hidden from untrusted, unapproved, and unauthorized parties.
This paper tackles the problem of leakless privacy preserving multi-keyword ranked search over encrypted cloud data (LRSE), and we solve the problem of search pattern, and co-occurrence (for the first time among multi-keywords SSE schemes) private information leakage. To capture the relevance between documents and the search query, we employ secure inner-product similarity that provides sufficient search accuracy[14]. In our approach, the documents and the search queries are described as binary vectors where each bit represents the existence of the corresponding keyword in the document/search query. Thus, the similarity can be measured by the inner-product of the query and document vector[14]. The distribution of the keywords in the documents is not uniform and decreases uncertainty (entropy) of the accessed documents. To address this problem, the key idea in our scheme is to exploit our chaining encryption notion to generate a variety of ciphertexts for high frequency keywords which leads to more uncertainty and a uniform probability model for the keywords distribution.
The contributions of this work are:
1. We explore the problem of leakless privacy preserving multi-keyword ranked search over encrypted cloud data. We build on a private model to prevent (without compromising efficiency):
(a) Search pattern attack (tracking the keywords searched by two or more queries)
(b) Co-occurrence attack (determining keywords with similar frequency)
2. Our methodological contribution is a novel chaining encryption notation which prevent the aforementioned attacks.
3. We demonstrate using privacy and security analysis the correctness of our proposed method.
To achieve our goals (see Section 2.1) there are two approaches. One possibility is to create an index which decreases the searches elapsed time. In the related literature two types of index are considered[4]: (1) building an index for each document Di[15]; (2) design an index which encompasses the entire corpus [10,16]. The alternative approach is to perform a sequential scan without an index. When the documents are large, an index will likely be faster than sequential search, but on the flip side, storing and updating the index increases overhead considerably. Either approach would be appropriate here depending on the corpus’s characteristics such as file length and file modification frequency.
We first describe the sequential search scheme using our novel chaining notion (see Section 4.1). Next we express our second scheme which benefits from an index for the whole corpus (see Section 4.2). Note that, in the second scheme we exploit the chaining notion idea in generating the index vectors even though it (chaining notion) is not employed to encrypt the documents.
1.1 System model
Our system model as illustrated in Figure 1, involves three different entities: data owner, data users, and cloud server. The data owner has a collection of documents 
(files) to be outsourced to the cloud server. Since files may contain sensitive information and the cloud server is not fully trusted, data must be encrypted (
); and any kind of information leakage that jeopardizes the data privacy is inadmissible. Moreover, for the sake of effective data utilization and to ensure precise results, the cloud server must apply the search requests (queries) on the encrypted data. Hence, before outsourcing the data onto the cloud, the data owner extracts a set of keywords Δd to build an encrypted searchable index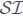 
. We extract the keywords before encrypting the data, so the keywords with a high frequency get encrypted into a number of ciphertexts. As a result, it becomes significantly more difficult for the cloud to track specific keywords in documents as we will explain shortly. Both the encrypted index and encrypted data are then transferred to the cloud server.
Figure 1. Architecture of the search over encrypted cloud data.
To search for files of interest, an authorized user first acquires a key K from the data owner through a search control mechanism such as broadcast encryption[4]. Upon receiving the encrypted search request q from a data user, the cloud server applies the request on the corresponding index 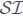and returns the results 
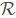(q). To increase result precision, the results are ranked based on their relevance to the request by the cloud server. Furthermore, to reduce the communication cost, the data user may send an optional number k along with q, so the cloud server only sends back the top-k documents that are most relevant to the search request[14].
The rest of this paper is organized as follows: Section 2 presents our threat model, design goals, and the preliminary. In Section 3, we describe the LRSE privacy requirements. Section 4 shows the proposed schemes in detail, followed by Section 5 which presents the privacy and security analysis. We summarize related works on privacy-preserving multi-keyword ranked search over encrypted cloud data in Section 6, and Section 7 summarizes our conclusions.
2 Problem formulation
2.1 Design goals
To address the aforementioned privacy issues (see Section 1), our design system should achieve privacy security and a high level of performance simultaneously with the following three goals:
● Leakless ranked search: For the sake of effective data retrieval and preserving privacy data users should be able to generate a leakless search query which reveals nothing more than the encrypted query.
● Privacy-preserving: Preventing the cloud server from learning additional information rather than seeing encrypted files, queries, and indexes is our highest goals. We describe the privacy requirements in Section 3.
● Efficiency: All of the above goals should be realized with a reasonable (or low) computation and communication overhead.
2.2 Preliminaries
Let = {D1,…, Dn} be a corpus of n documents, and id(Di) be the unique identifier of the of document Di. Let Δ be a dictionary of keywords with size m. Let Δd = {w1,…, wd} be the dictionary of the d words for the corpus such that Δd ⊆ Δ.
Definition 1. (Searchable Encryption). A multi-keyword Searchable Encryption (SE) scheme consists of 6 algorithms, SE = (KeyGen, BuildIndex, Encryption, Query, Search, Decryption) such that:
1. KeyGen (1λ): Taking a security parameter λ as an input and outputs a secret key K.
2. BuildIndex (): This algorithm takes in a corpus of documents = {D1,…, Dn} and generates an index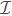 
.
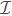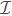3. Encryption (, , K): The encryption algorithm takes a document corpus , an index and a secret key K as input and outputs an encrypted document corpus 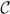= {C1,…, Cn}, and a secure index .
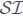4. Query (Δq, K): This algorithm takes a set of keywords Δq ⊆ Δd, and a secret key K as input, and generates an encrypted query q.
5. Search (q, 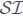): The search algorithm takes an encrypted query q and the secure index 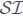as input, it outputs 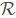(q) a set of document identifiers whose corresponding documents are the most relevant files to the query q.
6. Decryption (Ci, K): The decryption algorithm takes in an encrypted data file Ci ∈ 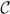and a secret key K as input, and outputs Di.
Definition 2. (History). Let be a document corpus. Let Δqi be a set of queried keywords of query qi. A history over is a tuple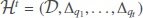 
over t queries.
The history is information that we are trying to hide from an adversary (cloud).
Definition 3. (Search Pattern). The search pattern over a history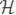 
t is a tuple, Ψ = (
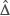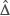q1,…,qt), over t queries where 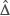qi, 1 ≤ i ≤ t is a set of encrypted keywords in the i-th query.
Definition 4. (Access Pattern). The access pattern over a history 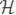t is a set, Ω = (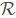(q1),…, 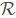(qt)) over t queries.
2.3 Threat model
We consider the cloud server an “honest-but-curious” entity in our model [4,9-11, 14]. This means the cloud server complies with the designated protocol (“honest”), but it is eager to collect more information by analyzing the encrypted data, message flows, and the index (“curious”). In our scheme, we assume that the cloud server knows the employed encryption and decryption methods, in addition to the encrypted documents 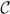and index 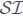. However, it does not know the key K. We are willing to leak document identifiers id(Di), 1 ≤ i ≤ n, encrypted queries and the access pattern defined in Definition 4. We can assume that the document sizes will also be leaked, but it can be trivially preserved by a “padding” method[4]. Thus, we classify the attack model to Known Ciphertext Attack in which the adversary only observes the ciphertext, i.e., encrypted documents 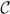, encrypted index 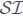, and queries.
3 Privacy requirements
To address security concerns and preventing a “honest-but-curious” server (see Section 2.3) from collecting users’ personal information, the data owner applies a symmetric key cryptography before outsourcing data to the cloud. Although cryptography impedes the cloud prying into the data owner’s private data, it cannot address all privacy concerns. Ideally, a cloud should learn nothing but the (encrypted) search results; and it jeopardizes data privacy and even security if the cloud deduces any information from the index, accessed files, queried keywords, etc. For example, by analyzing this information, the cloud server may infer the major subject of a document, or even the file’s content [17]. Therefore, methods must be designed to prevent the cloud from performing these kind of association attacks. Data privacy and index privacy are default requirements in the literature, and in the following, we enumerate more challenging and more complex privacy requirements.
1. Search Pattern Privacy: Uncovering the relation between two or more search requests can lead to more information leakage and data/user privacy violation. Also, the resultant documents, which are ranked based on the query q, provide a good opportunity for the cloud to identify the keywords and their corresponding outsourced documents. Disguising the search pattern from unauthorized parties is among the most complex challenges in this field, so related literature[10,11,18] has not yet addressed this completely issue.
2. Co-occurrence Keyword Privacy: Keywords with the same distribution pattern expose more privacy violation risks. In the other words, the privacy of the keywords that co-occur often are tied to each other, and compromising the privacy of one term can lead to privacy violation of the co-occurring term. As a result, the privacy level of co-occurring terms is lower than the regular terms in the same condition. Therefore, we should protect and hide this term dependency to protect the co-occurring terms or at least put them at the same level of privacy protection with singularly occurring terms.
4 LRSE scheme
To meet these requirements, we propose the LRSE scheme. LRSE is a privacy preserving multi-keyword ranked search mechanism over encrypted files. We adopt the secure inner product proposed by Wong et al.[14]. The index 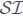and the query q are both protected using this encryption strategy.
The key idea in our approach is to generate a variety of ciphertexts for high frequency keywords from the corpus . Hence, multiple encrypted versions of a keyword will be used to search for the same keyword. This directly affects the search pattern ψ that the adversary collects to discover the keyword plaintext. We propose two schemes: Scheme I introduces a solution for searching with sequential scan using our novel chaining notation; and Scheme II, expresses how the chaining notion can be employed to handle controlled searching with an outsourced encrypted index.
4.1 Scheme I-sequential scan
Recall that in Definition 1 a searchable encryption scheme contains a suite of 6 algorithms. Here, we explain how each algorithm works in Scheme I. In the setup phase, beside calling the KeyGen to generate the secret key K, we generate a document-term matrix and a required ciphertext vector. Scheme I’s details are presented here:
● Setup. Let γ be a n × d document-term matrix(DTM) which an element ei j represents the frequency of keyword wj in document Di. Let φ = (l1,…, ld)be required-ciphertext vector which li, 1 ≤ i ≤ d shows the number of required ciphertext for keyword wi. We first extracts the corpus keyword dictionary Δd from the entire corpus and then generates the document-term matrix γ. Afterwards, we generate the the required-ciphertext vector φ (see below for more details).Then we call KeyGen algorithm to generate the secret key K that will be used to encrypt the documents.
● RequiredCiphertext. The probability of querying high frequency keywords is high, so these keywords are more prone to privacy leakages. In a strong attack model[12] where the cloud server is equipped with more knowledge such as the term frequency statistics, the attacker(cloud) can extract invaluable information form the encrypted files[16]. Moreover, by issuing each query to the cloud, the data user is revealing more private information such as her interests and hobbies. Thus, there are two main challenges: 1) hiding the keyword frequencies in the outsourced encrypted documents and 2) obscuring the frequency of the queried keywords which may lead to exposing the underlying keywords[12].
In an ideal world the keyword frequencies are equal, and the data user uniformly queries all of the available keywords. Thus, the cloud observation from the encrypted files and the queries does not leak any information. Although this is impossible in the real world, our goal is to break down the keyword frequencies to get close to the ideal scenario. For this reason we calculate the average of each column (average of each keyword in the document collection ). Note that because we are employing uniform distribution the average and the median are effectively the same. Let A = (a1,…, ad) be the average vector in which ai , 1 ≤ i ≤ d shows the average of keywords wi in corpus ; thus,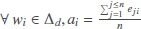 
.
To determine the number of required ciphertexts for each keyword (li) we define a new measure as threshold τ which is the floor of the minimum element in the average vector A. Finally, we determine the number of required-ciphertext vector φ by calculating the ceiling of the maximum frequency for each keyword in DTM-matrix γ divided by the threshold τ:
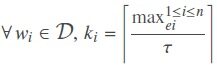
We divide the maximum frequency of each keyword by the minimum average of the keywords (threshold factor τ) to ensure each encrypted version will occur with the same frequency as the minimum value in the average vector A. With this strategy, the cloud (or an adversary) sees all of the encrypted keywords in the same frequency range. Thus, we gain more uncertainty and a higher level of entropy so identifying the keywords becomes more difficult for the cloud.
● GenerateCiphertext. Before we explain how we encrypt the documents, we define the BuildChain algorithm which will be used by the Encryption algorithm.
- BuildChain(K, Δd, φ). This algorithm takes a secret key K, a document keyword dictionary Δd, and a required-ciphertext vector φ as input. It outputs an encrypted keyword dictionary 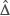dʹ = (ŵ11,…, ŵij) where ŵij is the j-th ciphertext of wi1≤i≤d and d′ is the number of encrypted keywords.
For each keyword wi ∈ Δd, BuildChain generates the first ciphertext ŵi1 by encrypting keyword wi using the secret key K. To generate the second ciphertext ŵi2, BuildChain encrypts XOR of previous ciphertext ŵi1 with keyword wi using the same secret key K (i.e., ŵi1
wi). Hence, each ciphertext is chained to the previous one. The algorithm continues generating new ciphertext for keyword wi until we have the expected number of ciphertexts according to the φ vector. Figure 2 shows the chaining process.
Note that compared to other approaches that adopt multiple keys[1], in our chaining methodology, we employ only one key for all of the required ciphertexts. This characteristic mitigates the key management challenges and lessen system costs during the key generation. Moreover, it enables the data users to generate the whole chain on their own side which reduces the communication costs and increases security and privacy. From the privacy viewpoint, keywords with a high frequency get encrypted multiple times (using chaining notion). As a result, it becomes significantly more difficult for the cloud to track down a specific keyword in a single document or across multiple documents.
We explain how Encryption algorithm (see Definition 1) works in LRSE. Note that, Scheme I is not an index-based method, so it does not need to take in an index 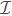(we will employ an index in Scheme II). After taking the inputs, Encryption algorithm call the BuildChain to generate the required-ciphertext vector φ. The BuildChain algorithm returns the encrypted keyword dictionary 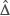d′ to the Encryption algorithm. Then Encryption algorithm starts to encrypt each document by fetching each word from the file and if the word is one of the keywords in Δd, we randomly choose one of its encrypted versions from 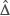d′, otherwise we encrypt the word with the secret key1. The subroutine “Add” in this algorithm adds the encrypted document (here Ci) to the encrypted file collection (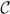). Algorithm 1 demonstrates how we encrypt each file.
Since the cloud sees the encrypted document collection 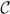, it generates the DTM matrix (γ′) based on the encrypted keywords in 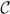. Thus, the number of columns in γ′ is d′ rather than d (d ≤ d′) and the high frequency keywords are eliminated in the whole matrix.
● GenerateQuery. In the initialization phase, the data owner and the data user exchange φ vector and the secret key K that enable the data user to make an encrypted query q. In addition, because we have multiple encrypted versions (ciphertexts) of each keyword, the data user can use a portion of the available ciphertexts for each keyword, but the data user must use the same portion for all of the keywords in the same query to not effect the results. For example, the data user may decide to use sixty percent of available ciphertext for each keyword, but he cannot employ sixty percent for the first keyword and forty percent for the second one, because it makes the results imprecise. Finally, encrypted query q is sent to the cloud. The data user may send an optional parameter k to the cloud to retrieve only the top-k resultant documents.
This is one of the characteristics that distinguishes our approach from other schemes. With each query the data user is able to randomly choose some of the ciphertext for each keyword which delivers more uncertainty and consequently more entropy. Thus, even if consecutive queries share some of their keywords, the cloud is not able to find a pattern between the queries due to using different versions of ciphertext in each query. Moreover, co-occurring terms appear with different ciphertext in the encrypted files, so, finding the co-occurring terms becomes significantly more difficult for the cloud.
The details of Query is shown in Algorithm 2. The data user declares the “portion” manually or it can be determined randomly by the algorithm (like we did in the Algorithm 2). This feature determines the percentage of each keyword ciphertext that will be employed in the query encryption process. For example, if wi possesses five different ciphertext and the portion is set to sixty percent, the algorithm employs three versions of the ciphertexts randomly for the current query. Moreover, the data user is able to generate the ciphertexts as all encrypted versions are chained together. Note that the plain query can be indicated by today’s web search engine such as Bing® and Google®, in which the data users tend to provide a sentence in natural languages or a set of keywords to express their intentions. In this case, we first extract the keywords Δq from the plain query.
● Search. Before explaining the LRSE search algorithm we define the document and query vector and the relevance score:
Definition 5. (Document Vector). Let Δd be the dictionary of keywords from corpus . A document vector Ti = (fw1,…, fwd) is a normalized vector that demonstrates the normalized frequency of each keyword fwj, 1 ≤ j ≤ d in document Di. Let T = {T1,…, Tn} be a set of all document vectors.
Definition 6. (Query Vector). A query vector Q is a d-element boolean vector such that ∀ 1 ≤ i ≤ d, Q[i] = 1 if wi ∈ Δq, and 0 otherwise.
Definition 7. (Relevance Score). Let Ti denote the normalized frequency vector of the document Di and Q be the query vector from Δq. Their relevance score si is inner product of document Di to query vector Q.
Recall that upon receiving the encrypted document collection 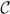the cloud builds its own DTM matrix γ′ and based on that it generates a set of encrypted document vectors 
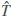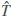= {1,…, 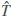n}. However, the cloud cannot make the real γ matrix and T (see Section 4.1). Upon receiving the encrypted query q, the cloud server executes Search algorithm. The LRSE Search(q, 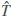, k) algorithm takes the encrypted query q, encrypted document vectors 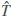, and an optional k, and returns the top-k encrypted resultant documents corresponding to 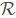(q) to the data user. Consider that the resultant documents are ranked according to their relevance score s.
● Decryption. The data user executes Decryption(Ci, K, 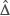d′) for each Ci in the resultant documents. This algorithm inputs an encrypted document Ci, a secret key K, and an encrypted keyword dictionary 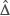d′, and outputs Di. Keywords in the resultant documents are encrypted randomly with a different encrypted piece of the chain. Thus, before decrypting the results, Decryption algorithm normalizes the results by changing each keywords ciphertext with the first ciphertext in the chain. It then decrypts the normalized encrypted document using the secret key K.
Figure 2. Chaining notion - generating multiple ciphertexts for each keyword.
4.2 Scheme II - Index
In Scheme II we employ an index structure to increase the search speed. In Scheme I we encrypt each document keyword by keyword, i.e., each block cipher contains one keyword (we consider each block large enough to store an encrypted keyword). In contrast, in Scheme II each block cipher contains 128 bits of a file (which may vary depend on the protocol and employed encryption scheme). Hence, the cloud learns nothing from the encrypted documents and is not able to generate its own γ′ matrix, so must to rely on the index (provided by the data owner) to find and rank the results.
Furthermore, the cloud is not able to learn the keyword positions in the documents. We also employ the secure asymmetric inner-product mechanism [14] which prevents the cloud from learning relevance score between two encrypted documents, and is only able to calculate the relevance score between the encrypted query vector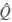 
and encrypted document vectors 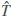. The following describes scheme II in detail:
● Setup. This part of the scheme consists of the same steps as Scheme I. We first extracts the corpus keyword dictionary Δd from the entire corpus and then generates the document-term matrix γ. Afterwards, we generate the required-ciphertext vector φ. In contrast with Scheme I we do not need to actually apply Algorithm 1 and generate multiple ciphertexts for each keyword wi. Instead, we apply the concept of the chaining notion on the document vectors and represent high frequency keywords with more than one element in the document vectors. For example, assume φi = 5, so keyword wi is represented with 5 positions in the document vectors. This property has less system cost and improves the system efficiency. Then we call KeyGen algorithm to generate a secret key K that will be used to encrypt the documents.
● KeyGen. The key generation algorithm is slightly different from the previous scheme. Beside a secret key K, the KeyGen should create a (d′ × d′) invertible random matrix m where d′ is the sum of all elements in φ (i.e. all of needed encrypted versions). The data owner runs KeyGen(1λd′) algorithm. The LRSE KeyGen algorithm takes in a security parameter λ and a number d’ and it returns a secret key K and an invertible (d′×d′) matrix m. This matrix will be used to encrypt the query and document vectors, so like the secret key, it should be protected.
● BuildIndex. The LRSE BuildIndex(, φ) takes in a document corpus and a required-ciphertext vector φ and outputs the plain index 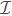. This algorithm first generates a normalized document vector Ti for each document Di based on tf-idf mechanism[19]. Note that each keyword wi is presented with multiple positions in the document vector based on value of φi. Then using the document vector set T, the algorithm builds a plain index. We adopt a tree-based index structure called keyword balanced binary (KBB) tree proposed by Xia et al. [16] Their secure index structure uses a “Greedy Depth-First Search(GDFS)” algorithm to find the most related nodes (documents) to the query.
In the KBB tree, each node u consists of 5 elements: node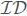 
, two pointers to the left and right child of node u, document 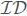(set to null in case u is an internal node), and the last element is a vector Ti that denotes the normalized “t f×idf” values of the keywords in the document Di. If u is an internal node, each element in vector Ti gets the maximum value of the corresponding keyword among u’s child nodes.
In the index construction phase, we generate a node for each document in the corpus. These nodes are the index tree’s leaves. The internal nodes are generated by generating a parent node for each two nodes (same strategy we apply to build a balanced binary tree). The parent node gets the highest value from its children for each element in its Ti vector.
Figure 3 provides an example of the index tree that is applied in our approach. The corpus in this example consists of 6 files(documents) f1,…, f6 and 4 keywords(cardinality of the dictionary d = 4). Assuming the query vector Q is equal to (0,0.83,0,0.24) and parameter k is set to 3 (i.e. number of documents returned to the data user). The figure shows the search process. The search process starts from the root node n and calculates the relevance score of the n11 (1.07) and n12 (0.428) to the query vector and moves to the n11 due to its higher relevance score. The search continues and reaches leaf node f4 with relevance score of 1.07 and then reaches f3 and f2 with 1.127 and 0.498 relevance scores, respectively. Afterwards, the search algorithm gets to the f1 with 0.524 relevance score and replace f3 in the result list (because we should return the top-3 relevant files and f1 relevance score is higher than f3 score). Finally, the search algorithm goes back to n12 node (based on Depth First Search algorithm) and stops there because the relevance score of the n12 (0.428) is less than the minimum relevance score (0.524) in the result list. Note that in practice T and Q vectors are encrypted using secret key K and matrix m. We refer the reader to Xia et al.[16] for more information about the index structure.
● GenerateCiphertext. The LRSE Encryption(, , 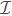m, K) algorithm takes a document collection D, a plain index 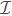, a secret matrix m, and a secret key K. The algorithm encrypts all of the documents in using the secret key K. To encrypt the index 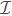, we adopt the secure asymmetric inner product by Wong et al.[14]. The algorithm can make the cloud server compute the inner product of two encrypted vectors 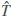i and 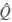without revealing any information about the actual values of them. Accordingly the encrypted subindex is built as {mTTi} where m is the random matrix that the data owner generates through running KeyGen algorithm. After encrypting the index 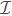and document corpus , the data owner performs a random shuffle on the encrypted document vectors, ensuring that the order of the encrypted entries do not reveal any information about the underlying data. The data owner then transfers the encrypted index and documents to the cloud.
● GenerateQuery. The Query(Δq, K, φ) algorithm is similar to Query algorithm in Scheme I (see Section 4.1), except in the last step, instead of sending the encrypted query q, it builds the corresponding query vector and generates the encrypted query vector 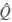by performing {m−1 Q}. It shuffles the encrypted query vector in the same way that the document vectors are shuffled and sent it to the cloud. The data user may send an optional parameter k to the cloud to retrieve only the top-k resultant documents.
● Search. Upon receiving the encrypted query 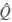, the cloud server runs Search(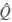, , 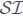k) algorithm which takes in an encrypted query vector 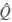, an encrypted index 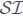and an optional parameter k. The Search algorithm finds the top-k resultant documents using the tree-based index 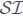. To gain the relevance score we calculates the inner product of the encrypted document vector in the encrypted query vector.
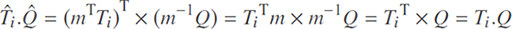
Note that the cloud server only learns the relevance score (similarity) of the documents to the query, while deducing the similarity between encrypted documents is not possible[14]. Finally, the cloud server returns the top-k resultant files to the data user.
● ResultDecryptor. In contrast with Scheme I, in this scheme we do not need to normalize the encrypted resultant documents so we achieve lower system cost and faster decryption. The LRSE Decryption(Ci, K) algorithm inputs an encrypted document and the secrets key k and outputs the document Di. The data user simply call the Decryption algorithm for each encrypted document in the resultant documents.
Figure 3. An example of the index tree that is employed in our approach.
5 Privacy and performance analysis
Our main goal in this section is to prove the proposed schemes in Section 4 provide privacy and security, as defined in Section 2.1. We also show that in comparison with related works, LRSE has an acceptable complexity in various criteria among previous SSE schemes (see Table 1). This property along with preserving the search pattern and co-occurring terms demonstrate the efficiency of our scheme.
Comparison of related works
| Properties | Curtmola et al[14](2011) | Cao et al[9](2014) | Liu et al[12](2014) | Xia etat[16](2016) | Guo et al[18](2018) | LRSE |
|---|---|---|---|---|---|---|
| Preserving access pattern | No | No | No | No | No | No |
| Server computation |  (1) | (n) | (n) | (n) | (n) | (n) |
| Server storage | (n) | (n) | (n) | (n) | (n) | (n) |
| Communication | (1) | (1) | (n) | (1) | (1) | (1) |
| Preserving search pattern | No | Yes | Yes | No | No | Yes |
| Preserving co-occurrence terms | No | No | No | No | No | Yes |
| Boolean/multi-keyword search | Boolean | Multi | Boolean | Multi | Multi | Multi |
In Section 4.1 we explained that to preserve the user privacy, our goal is to make the document and query vectors as uniform as possible (without compromising the efficiency). Hence, the cloud server is not able to distinguish the high frequency keywords in the encrypted documents. Entropy measure can evaluate the uniformity of document vectors and is employed in many approaches [20-22] to evaluate the privacy. By comparing the entropy of the LRSE document vectors with original ones we demonstrate higher entropy and consequently higher privacy of the document vectors generated by LRSE.
5.1 Entropy of LRSE Document Vectors
We prove that by expanding the document vectors using our approach, privacy and security of the outsourced data increases. Note that, adding dummy keywords[4,9] to extend the length of the data vectors does not necessarily ensure an increase of the security, and in some case it may even decrease the privacy and security of the outsourced data (see Example 1).
The main idea behind expanding/extending the length of the document vectors is to add more uncertainty to document and query vectors, which results in higher entropy. Although, adding to the length of the document vector can lead to higher entropy, in Example 1 we demonstrate that just extending the document vector’s length does not guarantee having a more uniform vector and higher entropy.
Example 1. Consider a document D1 with 3 keywords. Assume the frequency of each keyword in D1 is (2, 3, 4), so term-frequency(t f) vector is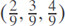 
. The entropy of this vector is equal to 1.06.
Now, to increase privacy and security to D1 we add a new dummy keyword with the frequency of 15. The modified frequency vector is (2, 3, 4, 15) and the new term-frequency(t f) vector is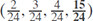 
The first impression is because of adding a dummy keyword, the entropy increases; however the entropy of the new vector is 1.059 which is less than the entropy of the original vector.
In Example 1 we showed that adding dummy keywords to the document/query vectors does not necessarily provide more security/privacy. Defining the property of the new dummy keywords that ensures higher entropy, are not considered in the related literature and we leave it as a future work. However, in Theorem 1 we prove that LRSE scheme provides more security/privacy.
Theorem 1. Given any document vector Ti for document Di valid in the LRSE scheme,
Proof. Consider:
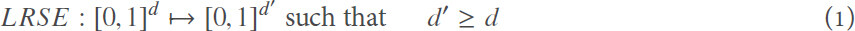
and
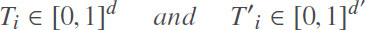
The entropy of the document vector Ti = (fwi,…, fwd) is:
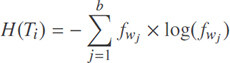
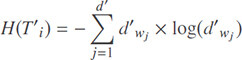
Recall φ = (l1,....,ld), with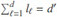 
, and for any fwj ∈ Ti we have:
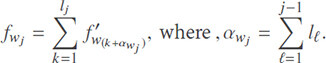
Hence:
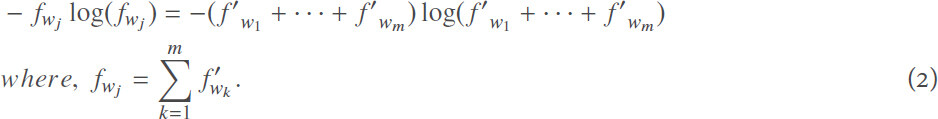
Moreover, note that log(x) is a monotonically increasing function and T′i possesses positive values (based on (1)), thus we have:
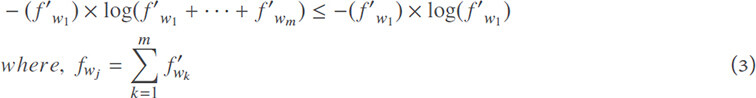
By extending the above inequality for all of the keyword frequencies in Ti and T′i:
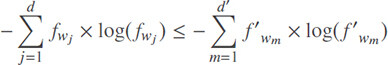
Thus we have:
□
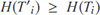
5.2 Privacy attacks
In Section 3 we identified two private information leakage (privacy attacks). In this section we explain how LRSE prevents search pattern and co-occurrence attack. Our schemes are not designed to preserve the user privacy against access pattern attack and we leave it as future work.
In LRSE with each query the data user is able to randomly choose a portion of the ciphertexts for each keyword. Thus, even if consecutive queries share some of their keywords, the cloud is not able to find a pattern between the queries due to using multiple versions of ciphertexts in each query. Further, co-occurring terms appear with different ciphertexts, so, finding the co-occurring terms becomes significantly more difficult for the cloud (see Section 4).
Assume, φi is the number of available ciphertexts for keyword wi, and in each query the query generator uses β percent of the φi. The number of possible permutations Γ that the query generator can employ is: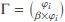 
.
For example, if we have φi = 10 available ciphertexts for keyword wi, and the query generator employs 40 percent of the ciphertexts in each query (β = 40%) the number of possible permutation is: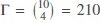 
. This means, there are 210 distinct possible choices for the query algorithm to ask for the same keyword. In other words, the probability of having 2 queries with same permutation of the ciphertexts for wi is 0.047% (
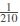). Note that the main idea is cloud sees all of the keywords are queried with the same probability even if the user starts requesting for the same keyword multiple times.
5.3 Result completeness
To apply the LRSE scheme we first extract keywords from documents in corpus. Technically, keywords with high frequency get extracted considering some linguistic knowledge to avoid stop words such as “the”, “for”, “if”, and etc.[23]. We then generate the φ vector based on the minimum value among the average of each keyword in the entire corpus. Further, we assume the random number generator is fair.
Considering all of the aforementioned, there is still a rare chance of incomplete results on the paper. Assume the term frequency of the keyword wi in document D is fi, and the number of the available ciphertexts for the corresponding keyword is φi. As long as fi ≥ φi there is no problem (case 1), because the corresponding C (encrypted D) contains all of the available ciphertexts and no matter which ciphertext versions are employed in the user query, C (and consequently D) will be placed among the possible results.
If fi ≤ φi the user query may contain encrypted versions of wi that do not exist in D (case 2). Recall that along with the query, the user also sends the parameter k to retrieve only the top-k documents. In case 2 if k is relativity less than the number of documents that includes wi there is still no problem because D’s relevance score to the query is very low and even if D had all of the encrypted versions of wi, it would not be placed among the top-k files (case 3). Note that number of documents that fi ≤ φi should be very low, otherwise the keyword extraction algorithm would not choose wi as a keyword in the first place.
The problem occurs when the user asks for all of the documents that includes keyword wi (case 4). In this condition, the results may be incomplete, because the user employs a portion of the available ciphertexts which may not be used in D. For example, consider we have a corpus with four documents (d1, d2, d3, d4), and the term frequency of keyword wi in each document is (25, 32, 6, 29). Also, consider that the number of available ciphertexts φi = 10 and the portion is set to forty percent for query q (e.g., forty percent of the available ciphertexts are employed to generate q by the query generator). Thus, the query generator randomly selects four versions of available ciphertexts (forty percent of φi). No matter what versions of the ciphertexts are employed in the query q, d1d2, and d4 will be placed among the possible results because the term frequency of keyword wi in those documents are greater than φi so those documents possess all of the available ciphertexts for wi (case 1). However, if fi ≤ φi (case 2), D3 may get excluded from the results due to not possessing the same versions that are employed in the query q. If k is set to 1,2, or 3, this issue does not effect the result accuracy because the user is only interested in the first top-k documents and d3 will not be placed in the top-k list. The problem occurs when users demands all of the documents containing wi (case 4).
To tackle this challenge (case 4), in Scheme I, we can inject the missed ciphertexts in the corresponding documents. In Scheme II, we do not even need to touch the encrypted documents; the only action is to adjust the corresponding document vectors regarding the missed ciphertexts. In order not to effect the relevance score, we employ the same strategy the related literature employs by adding dummy keywords while not affecting the relevance score[19,14].
5.4 Security
The secure asymmetric inner product[14] is widely used in many existing secure search schemes[19,10,16,18,24] and it has been proved to be secure in known ciphertext attacks. In this section we show that chaining the ciphertexts are not weakening the underlying secure symmetric encryption scheme; and we give the security proofs for the schemes presented in Section 4.
Definition 8. (Symmetric encryption scheme)[4]. A symmetric encryption scheme is a set of three polynomial-time algorithms (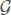
, ξ, ) such that 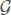takes an unary security parameter k and returns a secret key K; ξ takes a key K and n-bit message m and returns ciphertext c; D takes a key K and a ciphertext c and returns m if K was the key under which c was produced. We refer to Curtmola et al.[4] for formal definition of security for symmetric encryption schemes.
Definition 9. (Indistinguishability). Let G and E be two random variables distributed on {0, 1}n. A SSE scheme is indistinguishable secure if for all non-uniform probabilistic polynomial-time adversaries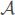 
: {0, 1}n → {0, 1}, for all polynomial “poly” and all sufficiently large k the distinguishable probability (also called advantage of adversary) is:
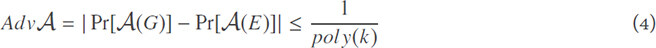
Definition 10. (Novel chaining notion). Let (, ξ, ) be an indistinguishable secure symmetric encryption scheme with ξ : {0, 1}k ×{0, 1}n → {0, 1}n. Let wi ∈ {0, 1}n be a keyword in the dictionary Δd. Given a natural number of ℓ The novel chaining notion of wi (NCN(wi)) is defined as:
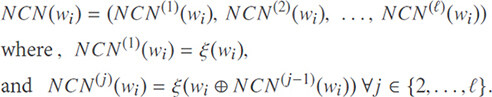
Theorem 2. The novel chaining notion is indistinguishable secure against known plaintext attack.
Proof. Let (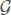, ξ, ) be the an indistinguishable symmetric encryption scheme. Moreover, recall ξ : {0, 1}k × {0, 1}n → {0, 1}n, so an encrypted vector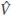 
is a valid vector as an input for ξ (because both encrypted (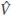) and plain (V) vectors are in {0, 1}n). Hence for any wi in the dictionary Δd and for any j, NCNj(wi) is in {0, 1}n. Since (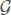, ξ, ) is indistinguishable secure scheme, the attacker is not able to find any relation between input and output except for a negligible amount[4], so the outputs is independent of the inputs, otherwise the encryption function (ξ) is not indistinguishable. Hence, keyword wi is independent from NCN(1)(wi) and NCN(1)(wi) is independent from NCN(2)(wi). Now we have to prove that every pair of the chains such as NCN(j)(wi) and NCN(j+i)(wi) is indistinguishable. By contradiction, let’s assume NCN(j)(wi) and NCN(j+i)(wi) are distinguishable, then even the pairwise NCN(j)(wi) and NCN(j+1)(wi) is distinguishable too, which is a contradiction. Therefore, NCN(.) is secure. □
Theorem 3. LRSE is an indistinguishable secure scheme against known ciphertext attack.
Proof. Let (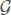, ξ, ) be an indistinguishable symmetric encryption scheme. Let the 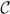= {ξ(Di), 1 ≤ i ≤ n} be the encrypted document collection. Let 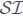be the encrypted searchable index, and let the NCN(.) be our secure chaining notion. Since (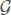, ξ, ) is indistinguishable secure the encrypted documents ξ(Di), 1 ≤ i ≤ n are indistinguishable secure from a random string {0, 1}*. Hence, the encrypted documents are indistinguishable secure. Further, the encrypted index and encrypted query vectors are secured using asymmetric inner product[14]. In Theorem 2 we proved that the NCN is indistinguishable secure, so chaining the ciphertexts does not weaken the symmetric encryption. Recall that in Scheme I we encrypt each file word by word using our novel chaining notion. In Scheme II we take advantage of the same idea in generating the document vectors and encrypt the documents block by block (instead of word by word). Thus, the encrypted documents ξ(Di), 1 ≤ i ≤ n, the index and the encrypted query vectors, and the novel chaining notion (NCN) are indistinguishable secure, so LRSE is indistinguishable secure. □
5.5 Efficiency and System Costs
Although two(multi) - party computation can address our designed goals, they suffer from low efficiency. They usually employ a n-path (in best case two-path) algorithm which means the retrieval phase needs two rounds of communication between the cloud server and data user[25]. Further, one of the biggest drawbacks is the complexity of the system and even for basic operations requires significantly more complicated computations.
Thus, scholars propose new methodologies to make a trade-off between privacy/security and efficiency. Table 1 compares LRSE with the previous work. In comparison with SSE schemes, LRSE preserves both the search pattern and co-occurring terms which are not supported in the multi-keyword SSE schemes.
Specifically, in comparison with Curtmola et al.[4] LRSE needs more sever computation, but LRSE supports multi-keyword search queries and also preserves the search pattern and co-occurring terms privacy which are not among Curtmola et al.[4] achievements. In compare with Cao et al. [9] LRSE preserves co-occurring terms. Both methods are at the same level of system costs, because in Cao et al.[9] work, to increase the privacy, length of the document vectors are extended with dummy keywords. In LRSE, we expand the length of the document vectors to increase the uncertainty and at the same time hide the search pattern and co-occurring terms (two birds with one stone). Moreover, in Section 6.1 we show that LRSE reaches a higher level result accuracy compared to Cao’s approach.
In comparison with a recent work[18], LRSE preserves search pattern and co-occurring terms privacy. Moreover, in Guo et al.’s[18] approach, a trusted proxy is considered in the system model which increases the system cost.
6 Implementation and analysis
We conducted a comprehensive experimental evaluation of LRSE on 203 English books[26] with more than five million words (excluding stop-words) and more than 2200 keywords. Our experiment includes a user and a server. Both entities are implemented using Java (JDK 1.8.0_111) and are executed on Windows 7 machines with Core2 Duo CPU at 3.17 GHz and 8 GBs of RAM. The user acts as the data owner and data user, and the server acts as the cloud server. We ran the experiments 10 times and difference between the maximum and minimum output of the same experiment was lees than 0.5%. For example, the result accuracy experiment showed less than a 0.2% difference in 10 runs.
Recall that in Section 4 we explained that the user’s query is a set of keywords or a sentence in natural language. We assumed that the number of keywords in each query is between five and ten. In other words, each time our query simulator is generating a random number in this range (5-10) which indicates the number of keywords in the corresponding query
Our analysis includes result accuracy and privacy assessment. In general, the cloud server observes two groups of vectors: document vectors and query vectors. Our experimental evaluation demonstrates a higher privacy in both groups, and a higher level of result accuracy compared with Cao’s result precision[9].
6.1 Result Accuracy
Section 4.1 describes a certain number of available ciphertexts (portion) are selected in every query. Although, the same portion for each keyword is employed in the query, it may effect the accuracy of the results due to the reason we explained in Section 5.3. Thus, there is a small chance to lose some result accuracy when the number of available ciphertexts for a keyword is bigger than its frequency in a specific document (because the encrypted versions that are employed in the document may differ from the ones in the query). In other words, when the cloud server returns the top-k documents based on their similarity to the query some of the real top-k relevant documents may be excluded.
This issue occurs in Cao’s [9] work when dummy keywords are inserted into each document vectors. conversely, to boost the privacy level, LRSE does not insert dummy keywords, instead we employ multiple ciphertexts to represents each keyword (based on their frequency) and for this reason (not adding noise to the document vectors) we expect to see higher level of result accuracy in LRSE. To evaluate the accuracy of the LRSE results we define the result accuracy Racc = ||(K′ ∩ K)||/||K|| where K and K′ are sets of expected result documents and documents retrieved by cloud server using LRSE. Additionally, ||A|| determines the number of elements in set A. Figure 4 and Figure 5 demonstrate our results.
Figure 4. Effect of portion on result accuracy over 5000 queries.
Figure 5. Result accuracy based on top_k over 5000 queries.
Recall that the “portion” determines percentage of each keyword ciphertext that will be employed in query encryption process (see Section 4.1). Figure 4 shows the effect of portion on result accuracy over 5000 queries. As the diagram shows LRSE achieves more than 91% result accuracy even when only 10% of the available ciphertexts are employed. Note that in our calculation in Section 5.2 we assumed 40% of the ciphertexts are employed and setting the portion to 10% increases the number of possible permutations and it becomes harder for the cloud server to analyze the access pattern. Moreover, increasing the portion from 10% to 20% raises the result accuracy around 5% and it gets to 95% which seems to be a reasonable trade-off to gain more result accuracy.
Figure 5 demonstrates the effect of top-k on the result accuracy. As the figure shows LRSE achieves to more than 98% result accuracy for top-3 documents. Top-10 or top-15 seems to be a reasonable top-k in our simulation since we have 203 books in our dataset. Even if we consider top-20 (which is 10% of our repository), we have more than 97% result accuracy. In comparison to MRSE (Cao’s work), LRSE achieves a higher precision in results. In MRSE standard deviation (σ) plays an important role which can effect the result accuracy. The bigger the σ is, the less result accuracy we have and it becomes more difficult for the cloud server to obtain information about the user data. Although the σ is not a parameter to be set up in LRSE, we calculate the standard deviation of the document vectors after applying LRSE. The average of σ for document vectors in lRSE is 1.34 with minimum of 0.97. Compared to MRSE (when the σ is 1) LRSE is 7% more accurate than MRSE, and this difference becomes more if the average of LRSE’s σ decreases to 1.
In both LRSE and MRSE as the top-k increases, the result accuracy decreases. In MRSE, this is because of the dummy keywords which can effect the similarity scores (dummy keywords may reduce some document scores which are in the real top-k results or increase the score of some documents out of the real top-k results). In LRSE, with increasing top-k, documents with less relevance to the query are placed in the result set. The frequency of the queried keywords in some documents is insufficient to cover all of the available ciphertexts for the corresponding keyword. Thus when the query asks for the missed ciphertext versions, those documents do not get into the resultant set even when they contain the required keywords. In Section 5.3 we propose to inject the missed ciphertext versions to prevent this problem. However, the results show that LRSE loses less than 1% accuracy from top-3 to top-30, which is tolerable. More importantly, this happens to less relevant documents to the query.
6.2 Document Vectors
6.2.1 Entropy of Document Vectors
We employed Shanon entropy to calculate entropy of the original and LRSE document vectors: H(V) =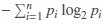 
, where V is the document vector, n is the number of keywords, and pi is probability of keyword i.
To calculate LRSE entropy progress, we define a measure as entropy improvement Himp = (H(Vli)–H(Voi))/H(Voi). where H(Vli) is the entropy of the document i vector in LRSE and H(Voi) is the entropy of the original document vector of the same document.
In Section 5.1 we proved that the entropy of document vectors which are generated by LRSE are greater than or equal to the entropy of original vectors.The simulation results emphasizes our theorem and shows at least a 25% entropy improvement in all of the documents and in some documents around 90%. Figure 6 demonstrates the first 20 documents entropy improvement.
Figure 6. Entropy improvement of the first 20 documents.
Note that, some documents such as “Document6” in Figure 6 may possess a high frequency of some keywords because specifically discuss a special topic. For example, legal terminologies are used heavily in the congress documents which increases their frequencies and drastically reduces the entropy of the document vectors and threatens owner/user privacy. In LRSE, we break down these high frequency occurrences to a couple of frequencies in the average frequency range (see Section 4.1). For example, assume the frequency of keyword wi in document Dj is 72 and the threshold is τ = 25, thus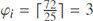 
. Hence, LRSE divides the wi frequency to 3 smaller parts (say 22, 24, 26) which are close to the frequency average (25), and then generates 3 ciphertexts using the chaining notion for each part. Because of this LRSE feature, our observation and result simulation show a 90% entropy improvement in some of the documents.
6.2.2 Standard Deviation of Document Vectors
A low standard deviation (σ) represents that most of the keyword frequencies are very close to the average and consequently to each other. Note that, the keywords can be deduced or identified in a strong attack model that the cloud server is equipped with more knowledge such as the term frequency statistics of the document collection[16]. For example, the frequency of economic terminologies is much higher than the other keywords in a budget document. Thus, the more keyword frequencies become closer to each other the more difficult identifying the keywords becomes.
Figure 7 demonstrates the standard deviation reduction of first 20 documents which are calculated by comparing the standard deviation of the original document vector and the corresponding vector in LRSE. The results show at least a 80%, σ reduction in each document. This means the frequency of the keywords are at least 80% closer to each other which preserve the data privacy against privacy attacks such as frequency statistical analysis mentioned above.
Figure 7. Standard deviation deduction in the first 20 documents.
6.3 Query Vectors
Although documents’ vectors are constant and barely change, the query vectors are prone to change as the user intentions and demands change. In other words, the number of queries increases over time, more information such as access pattern will be revealed to the cloud. For this reason, we dedicate the third part of our analysis to query vectors. The result analyses shows that LRSE protects the access pattern and privacy of the queries even when the number of queries grows.
6.3.1 Euclidean Distance from Ideal Vector
To preserve the access pattern, the ideal is the cloud server sees all of the queried keywords with the same frequency. In other words, after receiving m search requests the normalized vector of queries on n keywords is: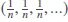 
, which means that to predict the next queried keywords or discovering the underlying plain keywords, the cloud server has no more chance than flipping a coin, which is the best case scenario.
We apply Euclidean distance measure to determine the distance between the ideal vector and the original/LRSE query vector. The less the Euclidean distance is, the closer we are to the ideal vector, and the more private is the data. To calculate the query vector, we processed the frequency of each queried keyword after every 3000 queries (for both original and LRSE queries). We then calculate its Euclidean distance from the ideal vector.
Figure 8 demonstrates the Euclidean distance improvement. The results show that the query frequency vector is at least 67% closer to the ideal vector after 30000 search requests submitted. Note that this is the minimum improvement due to using uniform distribution. We randomly select some keywords to create the queries. However in the real world users keep asking for documents in their field of expertise or their interests which makes the original frequency vector farther away from the ideal vector.
Figure 8. Euclidean distance improvement over 30000 queries.
6.3.2 Standard Deviation of Query Vectors
In Section 6.2.2 we explained the importance of having low standard deviation(σ) and analyzed the σ of LRSE document vectors. In this section we study the σ reduction of the query vectors. Unlike the documents, the number of the queries and consequently query vectors increases during the time and for this reason we show the σ reduction over time. We employed the same methodology in Section 6.2.2 to evaluate the standard deviation reduction.
Figure 9 demonstrates that LRSE reduces the standard deviation 25-30%. In other words, identifying the keywords are 30% more difficult using LRSE. Moreover the reduction amount stays in the same range (25%-30%) as the number of queries increases which shows the stability of LRSE.
Figure 9. Standard deviation improvement of the queries over 30000 queries.
7 Related work
The symmetric searchable encryption (SSE) introduced by Song et al.[1], where each word is encrypted under a particular two-layered encryption. Afterward, Goh[15] improved the search request time using Bloom filters. Chang et al.[3] and Curtmola et al.[4] then enhanced the security definitions, constructions and proposes some improvements. However, traditional symmetric encryption schemes only supports exact keyword search and cannot endure any kind of format inconsistency or minor imperfections. To address this issue, Li et al.[27] propose a method in which returned documents are designated according to the predefined keywords or the closest possible matching documents, based on keyword similarity semantics. Kuzu et al.[28] also tackle this challenge and propose a method with more efficiency and less overhead.
All these approaches support only Boolean search. Thus, finding the most relevant documents for the data user’s multi-keyword search request is a crucial challenge. To resolve this challenge, Cao et al.[9] introduce a method that allows data users to apply a multi-keyword search request on the encrypted files with ranking capability. Cao et al.[9] chose the similarity measure of “coordinate matching”, that is, as many matches as possible. And to capture the relevance of outsourced documents to the query keywords, the “inner product similarity” is employed. Later, Fu et al.[10] propose a model that makes the query results more personalized for each user based on their search history. Considering the user search history, they built a user interest model for individual users with the help of the semantic ontology WordNet. Moreover, Yu et al.[11] propose a user-ranked multi-keyword method to prevent data privacy leaks in cloud-ranked methods. They employed the vector space model and homomorphic encryption. The vector space model helps to provide sufficient search accuracy, whereas the homomorphic encryption enables users to get involved in the ranking procedure, while the remaining computing work is done on the server side. In a recent work, Guo et al.[18] propose a multi-keyword SSE approach which support multi data owners, and to tackle the key management challenges they exploit a trusted proxy.
However, these schemes function based on the symmetric key encryption, where the same key is employed to encrypt and decrypt the data. Another approach is to use public key encryption. Boneh et al.[2] defined the concept of the “public key encryption with keyword search”, and later, several methods [6,29-32] were introduced to improve the efficiency and system cost of the public-key searchable encryption schemes. Basically, these methods exercise one key for encryption and another key for decryption. Thus, data users who own the private key are able to search the outsourced data encrypted by the public key.
Nevertheless, all these methods suffer from private information leakage such as access pattern, search pattern, and co-occurrence information leakage. Cao et al.[9] believe that, to solve this problem, we must “touch” the whole outsourced dataset, which ends in losing the efficiency so other investigators chose not to impede these leaks which kept them out of the designed goals.
8 Conclusions
The problem of leakless preserving privacy multi-keyword ranked search in SSE schemes, addressed here. We built a private model to prevent two kinds of leakage: search pattern and co-occurrence private information leakage. We employed the asymmetric inner-product to calculate the relevance score of each document with respect to the query. We also introduced our chaining encryption notion to generate multiple ciphertexts for the same keyword. All this leads to more uncertainty and a uniform probability model for the keywords distribution. Furthermore, with our chaining encryption notion, the data user is able to randomly choose a portion of the ciphertexts for each keyword. Thus even if consecutive queries share some keywords, the cloud is not able to find a pattern between the queries due to using different versions of ciphertexts in each query. Moreover, co-occurring terms appear with different ciphertexts in the encrypted documents, and so, finding the co-occurring terms becomes significantly more difficult for the cloud. Next, to tackle the challenge of leakless multi-keyword ranked search, we propose the LRSE scheme and define the privacy requirements. In addition, we explain each level of the LRSE scheme in details and describe the required algorithms.
Furthermore, we performed the security and privacy analysis to show the efficiency of our proposed approach. We proved the the novel chaining notion and consequently LRSE is secure and compared complexity of our proposed scheme with related work in various criteria such as server computation, communication, etc. Looking to the future, we will modify LRSE to prevent access pattern attack.
Declarations
Authors’ contributions
Each author contributed equally to the paper.
Availability of data and materials
Not applicable.
Financial support and sponsorship
This research is partly supported by the Natural Sciences and Engineering Research Council of Canada.
Conflicts of interest
All authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2020.
REFERENCES
1. Song DX, Wagner D, Perrig A. Practical techniques for searches on encrypted data. Proceeding 2000 IEEE Symposium on Security and Privacy. S&P. 2000 Berkeley, USA. New York: IEEE; 2000.
2. Boneh D, Di Crescenzo G, Ostrovsky R, Persiano G. Public key encryption with keyword search. In: International conference on the theory and applications of crypto-graphic techniques Interlaken, Switzerland. Berlin: Springer; 2004. pp. 506-522.
3. Chang YC, Mitzenmacher M. Privacy preserving keyword searches on remote encrypted data. Proceedings of the Third international conference on Applied Cryptography and Network New York, USA. Berlin: Springer; 2005.
4. Curtmola R, Garay J, Kamara S, Ostrovsky R. Searchable symmetric encryption: improved defifinitions and effificient constructions. Proceedings of the 13th ACM conference on Computer and communications security Alexandria Virginia, USA. New York: J ComputSecur; 2006.
5. Golle P, Staddon J, Waters B. Secure conjunctive keyword search over encrypted data. In: International Conference on Applied Cryptography and Network Security Yellow Mountains, China. Springer, 2004; Berlin: Springer; 2004. pp. 31-45.
6. Liu Q, Wang G, Wu J. Secure and privacy preserving keyword searching for cloud storage services. J Netw Comput Appl 2012;35:927-33.
7. Cash D, Jarecki S, Jutla C, Krawczyk H, Roşu MC, et al. Highly-scalable searchable symmetric encryption with support for boolean queries. In: Advances in Cryptology–CRYPTO. 2013 Santa Barbara, USA. Berlin: Springer; 2013. pp. 353-373.
8. Gai K, Zhu L, Qiu M, Xu K, Choo KKR. Multi-access filtering for privacy-preserving fog computing. IEEE Trans on Cloud Comput 2019:1-1.
9. Cao N, Wang C, Li M, Ren K, Lou W. Privacy-preserving multi-keyword ranked search over encrypted cloud data. IEEE Trans Parallel Distrib Syst 2014;25:222-33.
10. Fu Z, Ren K, Shu J, Sun X, Huang F. Enabling personalized search over encrypted outsourced data with efficiency improvement. IEEE Trans Parallel Distrib Syst 2016;27:2546-59.
11. Yu J, Lu P, Zhu Y, Xue G, Li M. Toward Secure Multikeyword Top-k Retrieval over Encrypted Cloud Data. IEEE Trans Dependable Secure Comput 2013:239-50.
12. Liu C, Zhu L, Wang M, Tan Ya. Search pattern leakage in searchable encryption: Attacks and new construction. Inf Sci 2014;265:176-88.
13. Perc M. Evolution of the most common English words and phrases over the centuries. J R Soc Interface 2012:rsif20120491.
14. Wong WK, Cheung DW, Kao B, Mamoulis N. Secure knn computation on encrypted databases. In: Proceedings of the 2009 ACM SIGMOD International Conference on Management of data Rhode Island, USA. New York: ACM; 2009. pp. 139-152.
15. Goh EJ. Secure indexes. Cryptology ePrint Archive, Report 2003/216. Avialable from: http://eprint.iacr.org/2003/216/. [Last accessed on 25 Sep. 2020].
16. Xia Z, Wang X, Sun X, Wang Q. A Secure and Dynamic Multi-Keyword Ranked Search Scheme over Encrypted Cloud Data. IEEE Trans Parallel Distrib Syst 2016;27:340-52.
17. Zerr S, Demidova E, Olmedilla D, Nejdl W, Winslett M, et al. Zerber: r-confifidential indexing for distributed documents. In: Proceedings of the 11th international conference on Extending database technology: Advances in database technology Nantes, France. New York: ACM; 2008. pp. 287-298.
18. Guo Z, Zhang H, Sun C, Wen Q, Li W. Secure multi-keyword ranked search over encrypted cloud data for multiple data owners. J Syst Softw 2018;137:380-95.
19. Ramos J. Using tf-idf to determine word relevance in document queries. In: Proceedings of the first instructional conference on machine learning, vol. 242. New Jersey, USA; 2003. pp. 133-42.
20. Begum RS, Sugumar R. Novel entropy-based approach for cost-effective privacy preservation of intermediate datasets in cloud. Cluster Computing 2019;22:9584-88.
21. Niu B, Li Q, Zhu X, Cao G, Li H. Enhancing privacy through caching in location-based services. In: 2015 IEEE conference on computer communications (INFOCOM) Hong Kong, China. New York: IEEE; 2015. pp. 1017-1025.
22. Palanisamy B, Liu L. Mobimix: Protecting location privacy with mix-zones over road networks. In: 2011 IEEE 27th International Conference on Data Engineering Hannover, Germany; New York: IEEE; 2011. pp. 494-505.
23. Hulth A. Improved Automatic Keyword Extraction given More Linguistic Knowledge. In: Proceedings of the 2003 Conference on Empirical Methods in Natural Language Processing. EMNLP ’03. USA: Association for Computational Linguistics; 2003. p. 216–223. Available from: https://doi.org/10.3115/1119355.1119383.
24. Sun W, Wang B, Cao N, Li M, Lou W, et al. Privacy-Preserving Multi-Keyword Text Search in the Cloud Supporting Similarity-Based Ranking. In: Proceedings of the 8th ACM SIGSAC Symposium on Information, Computer and Communications Security. ASIA CCS ’13. New York, NY, USA: Association for Computing Machinery; 2013. p. 71-82. Available from: https://doi.org/10.1145/2484313.2484322.
25. Goldreich O, Ostrovsky R. Software protection and simulation on oblivious RAMs. Journal of the ACM (JACM) 1996;43:431-73.
26. Publication G. Archived Textbooks; Available from: https://www.gutenberg.org/ebooks. Last accessed: 27-August-2020.
27. J L, Q W, C W, N C, K R, et al. Fuzzy Keyword Search over Encrypted Data in Cloud Computing. In: 2010 Proceedings IEEE INFOCOM. San Diego, CA, USA; 2010. pp. 1-5.
28. Kuzu M, Islam MS, Kantarcioglu M. Effificient similarity search over encrypted data. In: Data Engineering (ICDE), 2012 IEEE 28th International Conference on Washington, USA; New York: IEEE; 2012. pp. 1156-67.
29. Bellare M, Boldyreva A, O’Neill A. Deterministic and effificiently searchable encryption. In: Annual International Cryptology Conference Santa Barbara, USA; Berlin: Springer; 2007. pp. 535-52.
30. Attrapadung N, Libert B. Functional encryption for inner product: Achieving constant-size ciphertexts with adaptive security or support for negation. In: International Workshop on Public Key Cryptography Paris, France; Berlin: Springer; 2010. pp. 384-402.
31. Boldyreva A, Chenette N, Lee Y, O’neill A. Order-preserving sym-metric encryption. In: Annual International Conference on the Theory and Applications of Crypto-graphic Techniques Cologne, Germany; Berlin: Springer; 2009. pp. 224-41.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Salmani K, Barker K. Leakless privacy-preserving multi-keyword ranked search over encrypted cloud data. J Surveill Secur Saf 2020;1:79-101. http://dx.doi.org/10.20517/jsss.2020.16
AMA Style
Salmani K, Barker K. Leakless privacy-preserving multi-keyword ranked search over encrypted cloud data. Journal of Surveillance, Security and Safety. 2020; 1(1): 79-101. http://dx.doi.org/10.20517/jsss.2020.16
Chicago/Turabian Style
Salmani, Khosro, Ken Barker. 2020. "Leakless privacy-preserving multi-keyword ranked search over encrypted cloud data" Journal of Surveillance, Security and Safety. 1, no.1: 79-101. http://dx.doi.org/10.20517/jsss.2020.16
ACS Style
Salmani, K.; Barker K. Leakless privacy-preserving multi-keyword ranked search over encrypted cloud data. J. Surveill. Secur. Saf. 2020, 1, 79-101. http://dx.doi.org/10.20517/jsss.2020.16
About This Article
Copyright
Data & Comments
Data
Cite This Article 12 clicks
Like This Article 18
likes
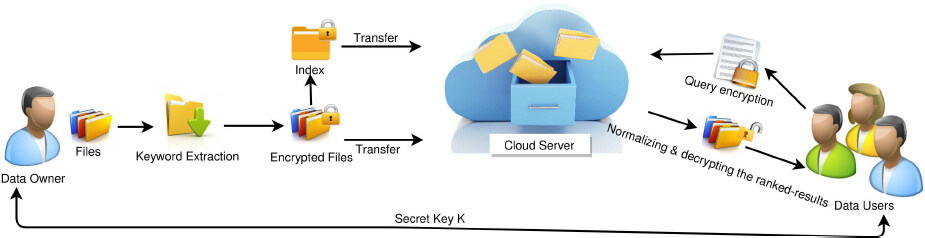
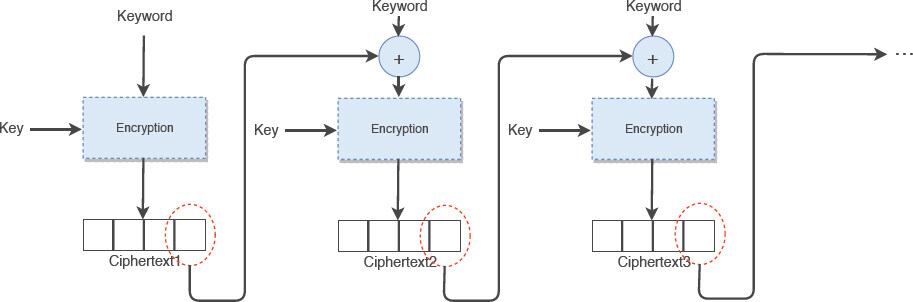
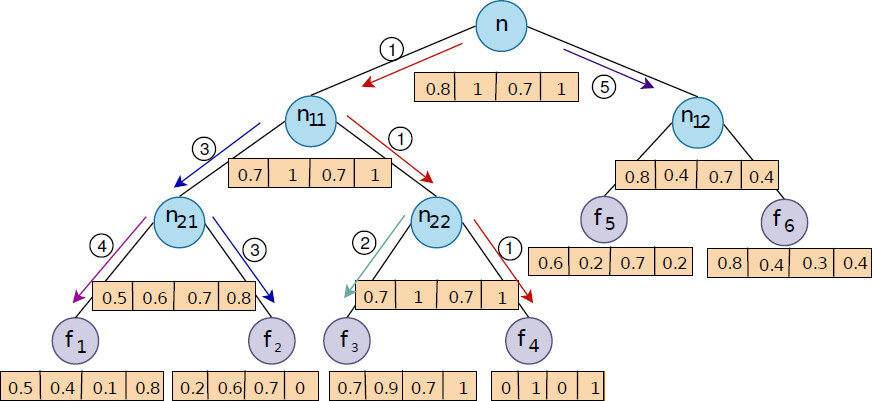
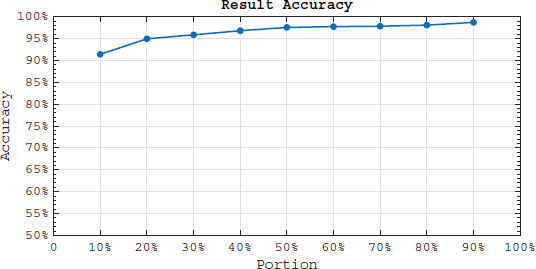
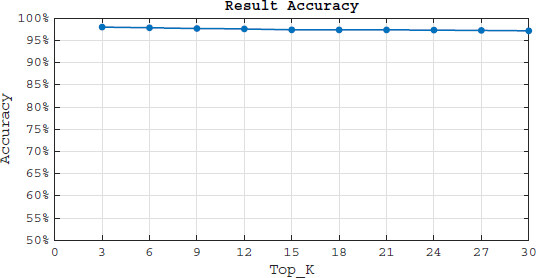
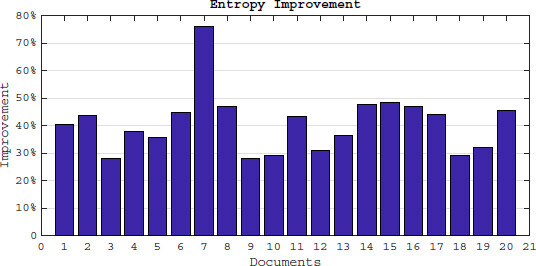
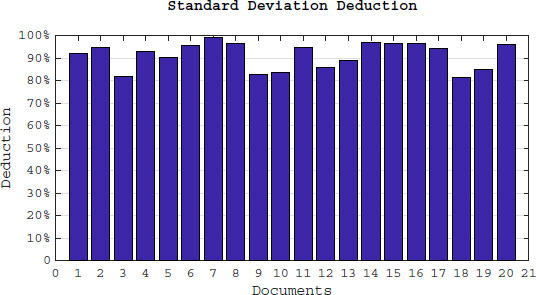
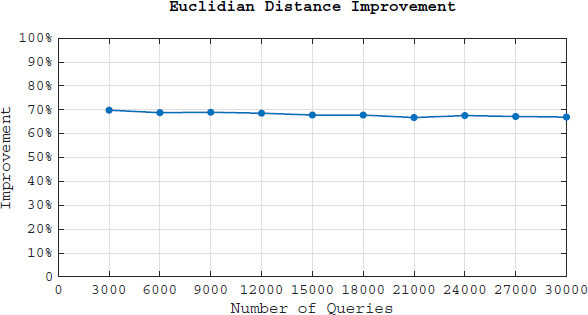
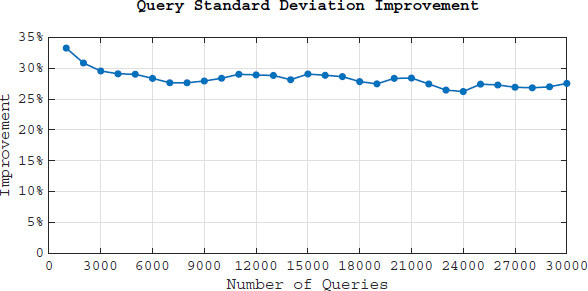
Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.